Question

【题目】如图，抛物线与轴交于两点，对称轴与轴交于点，点，点，点是平面内一动点，且满足是线段的中点，连结．则线段的最大值是________________．

Answer 1

【答案】

【解析】

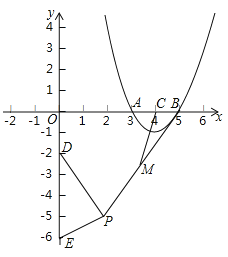
首先通过解方程得出点A的坐标，然后进一步根据抛物线性质得出点C为AB的中点，结合题意，利用勾股定理求出AQ，然后根据题意得出点P在以DE为直径的圆上，圆心Q点的坐标为(，0)，圆Q的半径为2，然后延长AQ较圆Q于点F，得出此时AF最大，再连接AP，利用三角形中位线性质进一步求解即可.

解方程可得，，

则：点A坐标为(3，0)，点B坐标为(5，0)，

∵抛物线的对称轴与轴交于点C，

∴点C为AB的中点，

设DE的中点为Q,则Q点的坐标为(，0)，

∴根据勾股定理可得：AQ=，

∵∠DPE=90°，

∴点P在以DE为直径的圆上，圆心Q点的坐标为(，0)，圆Q的半径为2，

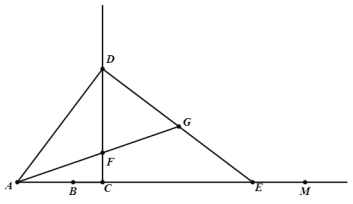
如图，延长AQ较圆Q于点F，此时AF最大，最大值为，

再连接AP，

∵点M是线段PB中点，

∴CM为△ABP的中位线，

∴CM=AP，

∴CM的最大值为：，

故答案为：.