题目内容
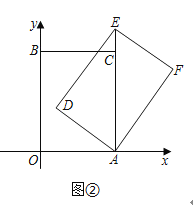
【题目】如图，射线AM上有一点B，AB＝6．点C是射线AM上异于B的一点，过C作CD⊥AM，且CD＝
AC．过D点作DE⊥AD，交射线AM于E. 在射线CD取点F，使得CF＝CB，连接AF并延长，交DE于点G．设AC＝3x．
（1） 当C在B点右侧时，求AD、DF的长．(用关于x的代数式表示)
（2）当x为何值时，△AFD是等腰三角形．
（3）若将△DFG沿FG翻折，恰使点D对应点
落在射线AM上，连接
，
．此时x的值为 （直接写出答案）
【答案】（1）
，
；（2）△ADF为等腰三角形，x的取值可以是
，
，
； （3）4或
【解析】
（1）由已知条件可得：CD=4x，根据勾股定理得：AD=5x，由AB=6且C在B点右侧，可以依次表示BC、CF、DF的长；（2）分两种情况：①当C在B点的右侧时，AF=DF，②当C在线段AB上时，又分两种情况：i）当CF＜CD时，如图3，ii）当CF＞CD时，如图4，由AF=DF，作等腰三角形的高线FN，由等腰三角形三线合一得：AN=ND=2.5x，利用同角的三角函数列比例式可求得x的值；（3）由翻折性质得到DG=
，
，从而证出
，从而推出∠FAC=∠DAG，即AF平分∠DAC，过F作FN⊥AD于N，分两种情况：当C在AB的延长线上时，当C在AB边上时，根据
可列出关于x的比例式，即可求解.
⑴∵CD＝AC，AC=3x，
∴CD=4x，
∵CD⊥AM，
∴∠ACD=90°，
由勾股定理得：AD=5x，
∵AB=6，C在B点右侧，
∴BC=AC-AB=3x-6，
∵BC=FC=3x-6，
∴DF=CD-FC=4x-（3x-6）=x+6；
（2）分两种情况：
①当C在B点的右侧时，
∴AC＞AB，
∴F必在线段CD上，
∵∠ACD=90°，
∴∠AFD是钝角，若△ADF为等腰三角形，只可能AF=DF，过F作FN⊥AD于N，如图，
∴AN=ND=2.5x，
∴
，
即
，
解得，
；
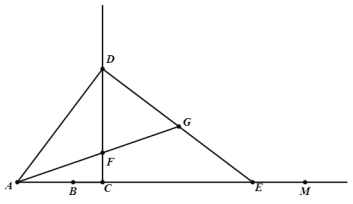
②当C在线段AB上时，同理可知若△ADF为等腰三角形，只可能AF=DF，
i）当CF＜CD时，过F作FN⊥AD于N，如图，
x的取值可以是，，；
∵AB=6，AC=3x，
∴BC=CF=6-3x，
∴DF=4x-（6-3x）=7x-6，
∵，
∴
，
解得
；
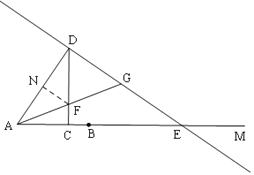
ii）当CF＞CD时，如图4，
BC=CF=6-3x，
∴FD=AD=6-3x-4x=6-7x，
则6-7x=5x，x=，
综上所述，x的取值可以是，，；
（3）∵△DFG沿FG翻折得到
∴DG=，
又∵AG=AG，
∴
∴∠FAC=∠DAG，
即AF平分∠DAC，
如图， 当C在AB的延长线上时，过F作FN⊥AD于N， FN=FC=3x-6，DF=x+6，
，
解得：x=4；
当C在AB边上时，如图，
∵FN=FC=6-3x， DF=7x-6，
∴
，
解得
；
综上所述，x的值是4或.
