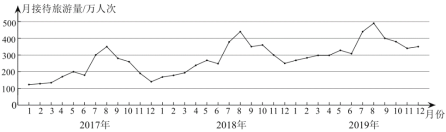
题目内容
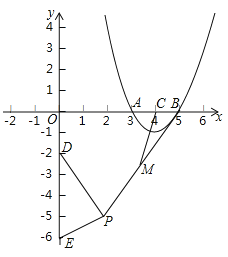
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
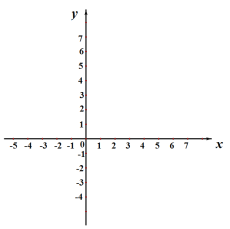
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)将A点横坐标,代入直线l:y=9x+14得到A点的坐标,再代入到抛物线中,即可求解;
(2)①将B点横坐标,代入直线l:y=9x+14得到B点的坐标,再代入到抛物线中,可求出抛物线的解析式;
②抛物线的顶点为N(![]() ),开口向下,C(b,5),B(-1,5),要使得抛物线M与线段BC有交点,N不在C的下方,即
),开口向下,C(b,5),B(-1,5),要使得抛物线M与线段BC有交点,N不在C的下方,即![]()
![]() 0,则分
0,则分![]() ,或
,或![]() 两种情况讨论,结合图象求解.
两种情况讨论,结合图象求解.
解:(1)∵抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2,
∴A(-2,-4),
代入y=-x2+2bx+c得![]() ,
,
∴![]() .
.
故答案为:![]() .
.
(2)∵点B在直线l:y=9x+14上,且B的横坐标为-1,
∴B(-1,5),
①若抛物线M:y=-x2+2bx+4b还过点B(-1,5),
∴![]() ,
,
∴b=3,
∴该抛物线的解析式:![]() ;
;
②∵![]() 的顶点为N(
的顶点为N(![]() ),开口向下,
),开口向下,
其中C(b,5),B(-1,5),
要使得抛物线M与线段BC有交点,N不在C的下方,即![]() 0,
0,
∴![]() ,或
,或![]() ,
,
当![]() 时,
时,
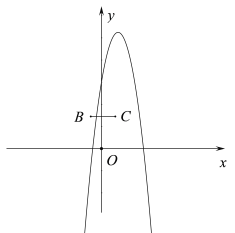
结合函数图象,若抛物线M与线段BC恰有一个交点,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
当![]() 时,
时,
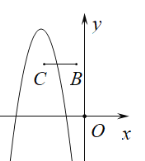
结合函数图象,若抛物线M与线段BC恰有一个交点,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
综上所述:抛物线M与线段BC恰有一个交点时,![]() 或
或![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目