Question

【题目】为了解学生在假期中的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目“进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图．

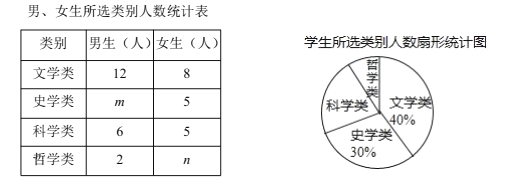
（1）m＝__________，n＝__________；

（2）扇形统计图中“科学类”所对应扇形圆心角度数为__________°；

（3）从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率．

Answer 1

【答案】（1）10，2；（2）79.2；（3）．

【解析】

（1）用文学类的人数除以所占的百分比求出抽查的总人数，再根据史学类所占的百分比即可求出m，再用总人数减去其它类别的人数即可求出n；
（2）用360°乘以“科学类”所占的比例，即可得出其所占圆心角的度数；
（3）根据题意列表得出所有等情况数和所选取的两名学生都是男生的情况数，然后根据概率公式即可得出答案．

解：（1）抽查的总学生数是：（12+8）÷40%=50（人），
m=50×30%-5=10，n=50-20-15-11-2=2；
故答案为：10，2；

（2）扇形统计图中“科学类”所对应扇形圆心角度数为；

故答案为：79.2；

（3）列表得：

	男1	男2	女1	女2
男1	--	男2男1	女1男1	女2男1
男2	男1男2	--	女1男2	女2男2
女1	男1女1	男2女1	--	女2女1
女2	男1女2	男2女2	女1女2	--

由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中所选取的两名学生都是男生的有2种可能，

∴所选取的两名学生都是男生的概率为．