ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΡΨΑεΦ”ΙΛ≥ßΫΪΙΚΫχΒΡA–ΆΓΔB–ΆΝΫ÷÷ΡΨΑεΦ”ΙΛ≥…C–ΆΘ§D–ΆΝΫ÷÷ΡΨΑε≥ω έΘ§“―÷Σ“ΜΩιA–ΆΡΨΑεΒΡΫχΦέ±»“ΜΩιB–ΆΡΨΑεΒΡΫχΦέ…Ό10‘ΣΘ§«“ΙΚ¬ρ3ΩιA–ΆΡΨΑεΚΆ2ΩιB–ΆΡΨΑεΙ≤Μ®Ζ―120‘ΣΘ°
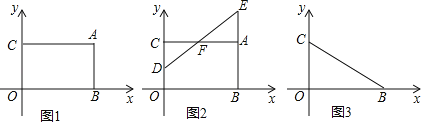
Θ®1Θ©A–ΆΡΨΑε”κB–ΆΡΨΑεΒΡΫχΦέΗς «Εύ…Ό‘ΣΘΩ
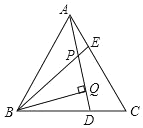
Θ®2Θ©ΗυΨί –≥Γ–η«σΘ§ΗΟΡΨΑεΦ”ΙΛ≥ßΨωΕ®”Ο≤Μ≥§Ιΐ2770‘ΣΙΚΫχA–ΆΡΨΑεΓΔB–ΆΡΨΑεΙ≤100ΩιΘ§»τ“ΜΩιA–ΆΡΨΑεΩ…÷Τ≥…1ΩιC–ΆΡΨΑεΓΔ2ΩιD–ΆΡΨΑεΘΜ“ΜΩιB–ΆΡΨΑεΩ…÷Τ≥…2ΩιC–ΆΡΨΑεΓΔ1ΩιD–ΆΡΨΑεΘ§«“…ζ≤ζ≥ωά¥ΒΡC–ΆΡΨΑε ΐΝΩ≤Μ…Ό”ΎD–ΆΡΨΑεΒΡ ΐΝΩΒΡ7/5Θ°
ΔΌΗΟΡΨΑεΦ”ΙΛ≥ß”–ΦΗ÷÷ΫχΜθΖΫΑΗΘΩ
ΔΎ»τC–ΆΡΨΑεΟΩΩι έΦέ30‘ΣΘ§D–ΆΡΨΑεΟΩΩι έΦέ25‘ΣΘ§«“…ζ≤ζ≥ωά¥ΒΡC–ΆΡΨΑεΓΔD–ΆΡΨΑε»Ϊ≤Ω έ≥ωΘ§ΡΡ“Μ÷÷ΖΫΑΗΜώΒΟΒΡάϊ»σΉν¥σΘ§«σ≥ωΉν¥σάϊ»σ «Εύ…ΌΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©A–ΆΡΨΑεΒΡΫχΦέΈΣ20‘ΣΘ§B–ΆΡΨΑεΒΡΫχΦέΈΣ30‘ΣΘΜΘ®2Θ©ΔΌΗΟΡΨΑεΦ”ΙΛ≥ßΙ≤”–3÷÷ΫχΜθΖΫΑΗΘ§ΖΫΑΗ1ΘΚΙΚΫχ23ΩιA–ΆΡΨΑεΘ§77ΩιB–ΆΡΨΑεΘΜΖΫΑΗ2ΘΚΙΚΫχ24ΩιA–ΆΡΨΑε76ΩιB–ΆΡΨΑεΘΜΖΫΑΗ3ΘΚΙΚΫχ25ΩιA–ΆΡΨΑεΘ§75ΩιB–ΆΡΨΑεΘ°ΔΎΖΫΑΗ3ΙΚΫχ25ΩιA–ΆΡΨΑεΘ§75ΩιB–ΆΡΨΑεΜώΒΟΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ5625‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηA–ΆΡΨΑεΒΡΫχΦέΈΣx‘ΣΘ§B–ΆΡΨΑεΒΡΫχΦέΈΣy‘ΣΘ§ΗυΨίΓΑ“ΜΩιA–ΆΡΨΑεΒΡΫχΦέ±»“ΜΩιB–ΆΡΨΑεΒΡΫχΦέ…Ό10‘ΣΘ§ΙΚ¬ρ3ΩιA–ΆΡΨΑεΚΆ2ΩιB–ΆΡΨΑεΙ≤Μ®Ζ―120‘ΣΓ±Θ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎxΘ§yΒΡΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©ΔΌ…ηΙΚΫχmΩιA–ΆΡΨΑεΘ§‘ρΙΚΫχΘ®100©¹mΘ©ΩιB–ΆΡΨΑεΘ§ΗυΨίΙΚΫχ100ΩιΡΨΑεΒΡΉήΖ―”Ο≤Μ≥§Ιΐ2770‘Σ«“…ζ≤ζ≥ωά¥ΒΡC–ΆΡΨΑε ΐΝΩ≤Μ…Ό”ΎD–ΆΡΨΑεΒΡ ΐΝΩΒΡ![]() Θ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎmΒΡ“Μ‘Σ“Μ¥Έ≤ΜΒ» ΫΉιΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωmΒΡ»Γ÷ΒΖΕΈßΘ§ΫαΚœmΈΣ’ϊ ΐΦ¥Ω…ΒΟ≥ωΗςΫχΜθΖΫΑΗΘΜ
Θ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎmΒΡ“Μ‘Σ“Μ¥Έ≤ΜΒ» ΫΉιΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωmΒΡ»Γ÷ΒΖΕΈßΘ§ΫαΚœmΈΣ’ϊ ΐΦ¥Ω…ΒΟ≥ωΗςΫχΜθΖΫΑΗΘΜ
ΔΎΗυΨίάϊ»σΘΫœζ έ ’»κ©¹≥…±ΨΘ§Φ¥Ω…Ζ÷±π«σ≥ω»ΐΗωΖΫΑΗΜώΒΟΒΡάϊ»σΘ§±»ΫœΚσΦ¥Ω…ΒΟ≥ωΫα¬έΘ°
Θ®1Θ©…ηA–ΆΡΨΑεΒΡΫχΦέΈΣx‘ΣΘ§B–ΆΡΨΑεΒΡΫχΦέΈΣy‘ΣΘ§
“άΧβ“βΘ§ΒΟΘΚ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ°
Θ°
¥πΘΚA–ΆΡΨΑεΒΡΫχΦέΈΣ20‘ΣΘ§B–ΆΡΨΑεΒΡΫχΦέΈΣ30‘ΣΘ°
Θ®2Θ©ΔΌ…ηΙΚΫχmΩιA–ΆΡΨΑεΘ§‘ρΙΚΫχΘ®100©¹mΘ©ΩιB–ΆΡΨΑεΘ§
“άΧβ“βΘ§ΒΟΘΚ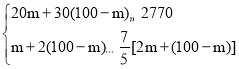 Θ§
Θ§
ΫβΒΟΘΚ23ΓήmΓή25Θ°
ΓΏmΈΣ’ϊ ΐΘ§
ΓύmΘΫ23Θ§24Θ§25Θ§
ΓύΗΟΡΨΑεΦ”ΙΛ≥ßΙ≤”–3÷÷ΫχΜθΖΫΑΗΘ§ΖΫΑΗ1ΘΚΙΚΫχ23ΩιA–ΆΡΨΑεΘ§77ΩιB–ΆΡΨΑεΘΜΖΫΑΗ2ΘΚΙΚΫχ24ΩιA–ΆΡΨΑεΘ§76ΩιB–ΆΡΨΑεΘΜΖΫΑΗ3ΘΚΙΚΫχ25ΩιA–ΆΡΨΑεΘ§75ΩιB–ΆΡΨΑεΘΜ
ΔΎΖΫΑΗ1ΜώΒΟΒΡάϊ»σΈΣ30ΓΝΘ®23+2ΓΝ77Θ©+25ΓΝΘ®2ΓΝ23+77Θ©©¹20ΓΝ23©¹30ΓΝ77ΘΫ5615Θ®‘ΣΘ©Θ§
ΖΫΑΗ2ΜώΒΟΒΡάϊ»σΈΣ30ΓΝΘ®24+2ΓΝ76Θ©+25ΓΝΘ®2ΓΝ24+76Θ©©¹20ΓΝ24©¹30ΓΝ76ΘΫ5620Θ®‘ΣΘ©Θ§
ΖΫΑΗ3ΜώΒΟΒΡάϊ»σΈΣ30ΓΝΘ®25+2ΓΝ75Θ©+25ΓΝΘ®2ΓΝ25+75Θ©©¹20ΓΝ25©¹30ΓΝ75ΘΫ5625Θ®‘ΣΘ©Θ§
ΓΏ5615ΘΦ5620ΘΦ5625Θ§
ΓύΖΫΑΗ3ΙΚΫχ25ΩιA–ΆΡΨΑεΘ§75ΩιB–ΆΡΨΑεΜώΒΟΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ5625‘ΣΘ°

 ΜνΝΠΩΈ ±Ά§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗ
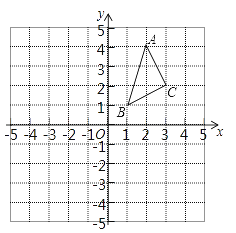
ΜνΝΠΩΈ ±Ά§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ”Ο“Μ―υ≥ΛΒΡ–ΓΡΨΑτΑ¥œ¬ΆΦ÷–ΒΡΖΫ Ϋ¥νΆΦ–Έ.
Θ®1Θ©Α¥ΆΦ ΨΙφ¬…ΧνΩ’ΘΚ
ΆΦ–Έ±ξΚ≈ | ΔΌ | ΔΎ | Δέ | Γ≠ |
–ΓΡΨΑτΒΡΗυ ΐ | 9 | Γ≠ |
Θ®2Θ©Α¥’’’β÷÷Ιφ¬…¥νœ¬»ΞΘ§¥νΒΎ![]() ΗωΆΦ–Έ–η“Σ________Ηυ–ΓΡΨΑτΘΜ
ΗωΆΦ–Έ–η“Σ________Ηυ–ΓΡΨΑτΘΜ
Θ®3Θ©«κ«σ≥ω¥νΒΎ100ΗωΆΦ–Έ–η“ΣΒΡ–ΓΡΨΑτΒΡΗυ ΐ.
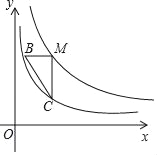
ΓΨΧβΡΩΓΩ”–![]() ΩπΑΉ≤Υ,“‘ΟΩΩπ
ΩπΑΉ≤Υ,“‘ΟΩΩπ![]() «ßΩΥΈΣ±ξΉΦ,≥§ΙΐΜρ≤ΜΉψΒΡΖ÷±π”Ο’ΐΓΔΗΚά¥±μ Ψ,Φ«¬Φ»γœ¬ΘΚ
«ßΩΥΈΣ±ξΉΦ,≥§ΙΐΜρ≤ΜΉψΒΡΖ÷±π”Ο’ΐΓΔΗΚά¥±μ Ψ,Φ«¬Φ»γœ¬ΘΚ
”κ±ξΉΦ÷ ΝΩΒΡ≤ν |
|
|
|
|
|
|
Ωπ ΐ |
|
|
|
|
|
|
(1)”κ±ξΉΦ÷ ΝΩ±»Ϋœ,![]() ΩπΑΉ≤ΥΉήΦΤ≥§ΙΐΜρ≤ΜΉψΕύ…Ό«ßΩΥΘΩ
ΩπΑΉ≤ΥΉήΦΤ≥§ΙΐΜρ≤ΜΉψΕύ…Ό«ßΩΥΘΩ
(2)»τΑΉ≤ΥΟΩ«ßΩΥ έΦέ![]() ‘Σ,‘ρ≥ω έ’β
‘Σ,‘ρ≥ω έ’β![]() ΩπΑΉ≤ΥΩ…¬τΕύ…Ό‘ΣΘΩ
ΩπΑΉ≤ΥΩ…¬τΕύ…Ό‘ΣΘΩ