Question

【题目】如图，平面直角坐标系中，点A在第一象限，AB⊥x轴于B．AC⊥y轴于C，A（4a，3a），且四边形ABOC的面积为48．

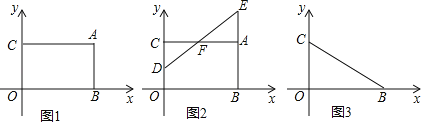
（1）如图1，直接写出点A的坐标；

（2）如图2，点D从O出发以每秒1个单位的速度沿y轴正半轴运动，同时点E从A出发，以每秒2个单位的速度沿射线BA运动，DE交线段AC于F，设运动的时间为t，当S△AEF＜S△CDF时，求t的取值范围；

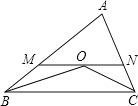
（3）如图3，将线段BC平移，使点B的对应点M恰好落在y轴负半轴上，点C的对应点为N，连BN交y轴轴于P，当OM＝3OP时，求点M的坐标．

Answer 1

【答案】（1）点A的坐标（8，6）；（2）t的取值范围为：0＜t＜2；（3）M（0，﹣）或（0，﹣18）．

【解析】

（1）根据矩形的面积列方程即可得到结论；

（2）过D作DH⊥AB于H，由S△AEF＜S△CDF，得到S矩形ACDH＞S△EDH，解不等式即可得到结论；

（3）如图3（1）和（2），设M（0，n），由平移的性质得N（﹣8，n+6），过N作NE⊥x轴于E，根据三角形和梯形的面积公式列方程即可得到结论．

（1）∵AB⊥x轴于B．AC⊥y轴于C，

∴四边形ABOC是矩形，

∵A（4a，3a），

∴AC＝4a，AB＝3a，

∴4a3a＝48，

∴a＝±2，

∵点A在第一象限，

∴a＝2，

∴点A的坐标（8，6）；

（2）如图2，过D作DH⊥AB于H，

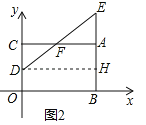
∵S△AEF＜S△CDF，

∴S△AEF+S梯形AFDH＜S△CDF+S梯形AFDH，即S矩形ACDH＞S△EDH，

∴8×（6﹣t）＞8×（6+t），

解得t＜2，

∴t的取值范围为：0＜t＜2；

（3）如图3（1）和（2），

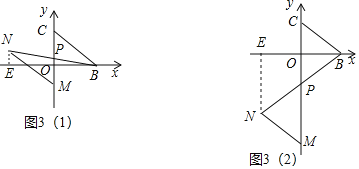
设M（0，n），由平移的性质得N（﹣8，n+6），

过N作NE⊥x轴于E，

∵S△BNE＝S梯形NEOP+S△POB，

∴（8+8）×|n+6|＝（OP+|n+6|）×8+8×OP，

解得：OP＝|n+6|，

∵OM＝3OP，

∴﹣n＝3×|n+6|，

解得：n＝﹣，n＝﹣18，

∴M（0，﹣）或（0，﹣18）．