ĢāÄæÄŚČŻ
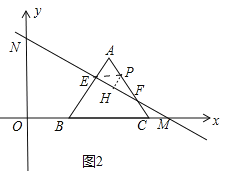
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬£¬Ö±ĻßMN·Ö±šÓėxÖį”¢yÖį½»ÓŚµćM£Ø6£¬0£©£¬N£Ø0£¬ ![]() £©£¬µČ±ß”÷ABCµÄ¶„µćBÓėŌµćOÖŲŗĻ£¬BC±ßĀäŌŚxÖįÕż°ėÖįÉĻ£¬µćAĒ”ŗĆĀäŌŚĻ߶ĪMNÉĻ£¬½«µČ±ß”÷ABC“ÓĶ¼lµÄĪ»ÖĆŃŲxÖįÕż·½ĻņŅŌĆæĆėløöµ„Ī»³¤¶ČµÄĖŁ¶ČĘ½ŅĘ£¬±ßAB£¬AC·Ö±šÓėĻ߶ĪMN½»ÓŚµćE£¬F£ØČēĶ¼2ĖłŹ¾£©£¬Éč”÷ABCĘ½Ņʵď±¼äĪŖt£Øs£©£®
£©£¬µČ±ß”÷ABCµÄ¶„µćBÓėŌµćOÖŲŗĻ£¬BC±ßĀäŌŚxÖįÕż°ėÖįÉĻ£¬µćAĒ”ŗĆĀäŌŚĻ߶ĪMNÉĻ£¬½«µČ±ß”÷ABC“ÓĶ¼lµÄĪ»ÖĆŃŲxÖįÕż·½ĻņŅŌĆæĆėløöµ„Ī»³¤¶ČµÄĖŁ¶ČĘ½ŅĘ£¬±ßAB£¬AC·Ö±šÓėĻ߶ĪMN½»ÓŚµćE£¬F£ØČēĶ¼2ĖłŹ¾£©£¬Éč”÷ABCĘ½Ņʵď±¼äĪŖt£Øs£©£®
£Ø1£©µČ±ß”÷ABCµÄ±ß³¤ĪŖ_______£»
£Ø2£©ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬µ±t=_______Ź±£¬MN“¹Ö±Ę½·ÖAB£»
£Ø3£©ČōŌŚ”÷ABCæŖŹ¼Ę½ŅʵÄĶ¬Ź±£®µćP“Ó”÷ABCµÄ¶„µćB³ö·¢£®ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÕŪĻßBA”ŖACŌĖ¶Æ£®µ±µćPŌĖ¶Æµ½CŹ±¼“Ķ£Ö¹ŌĖ¶Æ£®”÷ABCŅ²ĖęÖ®Ķ£Ö¹Ę½ŅĘ£®
¢Łµ±µćPŌŚĻ߶ĪBAÉĻŌĖ¶ÆŹ±£¬Čō”÷PEFÓė”÷MNOĻąĖĘ£®ĒótµÄÖµ£»
¢Śµ±µćPŌŚĻ߶ĪACÉĻŌĖ¶ÆŹ±£¬Éč![]() £¬ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öSµÄ×ī“óÖµ¼°“ĖŹ±µćPµÄ×ų±ź£®
£¬ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öSµÄ×ī“óÖµ¼°“ĖŹ±µćPµÄ×ų±ź£®

”¾“š°ø”æ£Ø1£©3£»£Ø2£©3£»£Ø3£©¢Łt=1»ņ![]() »ņ
»ņ![]() £»¢ŚS=
£»¢ŚS= ![]() £¬µ±t=
£¬µ±t=![]() Ź±£¬”÷PEFµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ
Ź±£¬”÷PEFµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ![]() £¬“ĖŹ±P£Ø3£¬
£¬“ĖŹ±P£Ø3£¬ ![]() £©£®
£©£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾Ż£¬”ĻOMN=30”ćŗĶ”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬ĒóÖ¤”÷OAMĪŖÖ±½ĒČż½ĒŠĪ£¬Č»ŗó¼“æÉµĆ³ö“š°ø£®
£Ø2£©Ņ×ÖŖµ±µćCÓėMÖŲŗĻŹ±Ö±ĻßMNĘ½·ÖĻ߶ĪAB£¬“ĖŹ±OB=3£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£»
£Ø3£©¢ŁČēĶ¼1ÖŠ£¬ÓÉĢāŅāBP=2t£¬BM=6©t£¬ÓÉ”÷PEFÓė”÷MNOĻąĖĘ£¬æɵĆ![]() =
=![]() »ņ
»ņ![]() =
=![]() £¬¼“
£¬¼“![]() =
=![]() »ņ
»ņ![]() =
=![]() £¬½ā·½³Ģ¼“æɽā¾öĪŹĢā£»
£¬½ā·½³Ģ¼“æɽā¾öĪŹĢā£»
¢Śµ±PµćŌŚEFÉĻ·½Ź±£¬¹żP×÷PH”ĶMNÓŚH£¬ČēĶ¼2ÖŠ£¬¹¹½Ø¶ž“ĪŗÆŹżĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹ¼“æɽā¾öĪŹĢā£»
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø1£©”ßÖ±ĻßMN·Ö±šÓėxÖįÕż°ėÖį”¢yÖįÕż°ėÖį½»ÓŚµćM”¢N£¬OM=6cm£¬ON=![]() £¬”ątan”ĻOMN=
£¬”ątan”ĻOMN=![]() =
=![]() £¬”ą”ĻOMN=30”ć£¬”ą”ĻONM=60”ć£¬”ß”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬”ą”ĻAOC=60”ć£¬”ĻNOA=30”ć£¬”ąOA”ĶMN£¬¼“”÷OAMĪŖÖ±½ĒČż½ĒŠĪ£¬”ąOA=
£¬”ą”ĻOMN=30”ć£¬”ą”ĻONM=60”ć£¬”ß”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬”ą”ĻAOC=60”ć£¬”ĻNOA=30”ć£¬”ąOA”ĶMN£¬¼“”÷OAMĪŖÖ±½ĒČż½ĒŠĪ£¬”ąOA=![]() OM=
OM=![]() ”Į6=3£®¹Ź“š°øĪŖ£ŗ3£®
”Į6=3£®¹Ź“š°øĪŖ£ŗ3£®
£Ø2£©Ņ×ÖŖµ±µćCÓėMÖŲŗĻŹ±Ö±ĻßMNĘ½·ÖĻ߶ĪAB£¬“ĖŹ±OB=3£¬ĖłŅŌt=3£®¹Ź“š°øĪŖ£ŗ3£®
£Ø3£©¢ŁČēĶ¼1ÖŠ£¬ÓÉĢāŅāBP=2t£¬BM=6©t£¬”ß”ĻBEM=90”ć£¬”ĻBME=30”ć£¬”ąBE=3©![]() £¬AE=AB©BE=
£¬AE=AB©BE=![]() £¬”ß”ĻBAC=60”ć£¬”ąEF=
£¬”ß”ĻBAC=60”ć£¬”ąEF=![]() AE=
AE=![]() t£¬µ±µćPŌŚEFĻĀ·½Ź±£¬PE=BE©BP=3©
t£¬µ±µćPŌŚEFĻĀ·½Ź±£¬PE=BE©BP=3©![]() t£¬ÓÉ
t£¬ÓÉ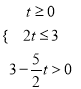 £¬½āµĆ0”Üt£¼
£¬½āµĆ0”Üt£¼![]() £¬”ß”÷PEFÓė”÷MNOĻąĖĘ£¬”ą
£¬”ß”÷PEFÓė”÷MNOĻąĖĘ£¬”ą![]() =
=![]() »ņ
»ņ![]() =
=![]() £¬”ą
£¬”ą![]() =
=![]() »ņ
»ņ![]() =
=![]() £¬½āµĆt=1»ņt=
£¬½āµĆt=1»ņt=![]() £®
£®
µ±µćPŌŚEFÉĻ·½Ź±£¬PE=BE©BP=![]() t-3£¬”ß”÷PEFÓė”÷MNOĻąĖĘ£¬”ą
t-3£¬”ß”÷PEFÓė”÷MNOĻąĖĘ£¬”ą![]() =
=![]() »ņ
»ņ![]() =
=![]() £¬”ą
£¬”ą![]() =
=![]() »ņ
»ņ![]() =
=![]() £¬½āµĆt=
£¬½āµĆt=![]() »ņ3£®”ß0”Üt”Ü
»ņ3£®”ß0”Üt”Ü![]() £¬ĒŅ
£¬ĒŅ![]() t-3£¾0£¬¼“
t-3£¾0£¬¼“![]() £¼t”Ü
£¼t”Ü![]() £¬”ąt=
£¬”ąt=![]() .
.
×ŪÉĻĖłŹö£¬t=1»ņ![]() »ņ
»ņ![]() £®
£®

¢Śµ±PµćŌŚEFÉĻ·½Ź±£¬¹żP×÷PH”ĶMNÓŚH£¬ČēĶ¼2ÖŠ£¬ÓÉĢāŅā£¬EF=![]() t£¬FC=MC=3©t£¬”ĻPFH=30”ć£¬”ąPF=PC©CF=£Ø6©2t£©©£Ø3©t£©=3©t£¬”ąPH=
t£¬FC=MC=3©t£¬”ĻPFH=30”ć£¬”ąPF=PC©CF=£Ø6©2t£©©£Ø3©t£©=3©t£¬”ąPH=![]() PF=
PF=![]() £¬”ąS=
£¬”ąS=![]() EFPH=
EFPH=![]() ”Į
”Į![]() t”Į
t”Į![]() =
= ![]() =
=![]() £¬”ß
£¬”ß![]() ”Üt”Ü3£¬”ąµ±t=
”Üt”Ü3£¬”ąµ±t=![]() Ź±£¬”÷PEFµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ
Ź±£¬”÷PEFµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ![]() £¬“ĖŹ±P£Ø3£¬
£¬“ĖŹ±P£Ø3£¬ ![]() £©£¬µ±t=3Ź±£¬µćPÓėFÖŲŗĻ£¬¹ŹPµćŌŚEFĻĀ·½²»³ÉĮ¢£®
£©£¬µ±t=3Ź±£¬µćPÓėFÖŲŗĻ£¬¹ŹPµćŌŚEFĻĀ·½²»³ÉĮ¢£®
¹ŹS= ![]() £¬µ±t=
£¬µ±t=![]() Ź±£¬”÷PEFµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ
Ź±£¬”÷PEFµÄĆ껿×ī“ó£¬×ī“óÖµĪŖ![]() £¬“ĖŹ±P£Ø3£¬
£¬“ĖŹ±P£Ø3£¬ ![]() £©£®
£©£®