题目内容
【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
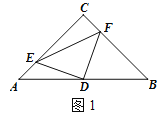
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
【答案】(1)△DEF是等腰直角三角形. (2)仍然成立.
【解析】试题分析:
(1)连接CD,如图1,结合已知条件易证△AED≌△CFD,由此即可证得DE=DF,∠EDF=90°,从而可得△DEF是等腰直角三角形;
(2)先根据题意画出符合要求的图形,如图2,连接CD,结合已知条件易证△AED≌△CFD,由此即可证得;DE=DF,∠EDF=90°,从而可得此时△DEF仍然是等腰直角三角形.
试题解析:
(1)△DEF是等腰直角三角形,理由如下:
如图1,连接CD,
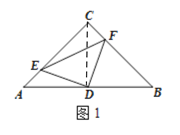
∵AC=BC,∠ACB=90°,点D是BC边的中点,
∴CD⊥BC,∠A=∠DCF=45°,CD=![]() BC=AD,
BC=AD,
又∵AE=CF,
∴△AED≌△CFD,
∴DE=DF,∠ADE=∠CDF,
又∵CD⊥BC,
∴∠CFD+∠CDE=∠ADE+∠CDE=∠CDA=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)如图2,(1)中结论仍然成立,理由如下:
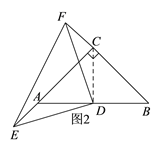
连接CD,∵AC=BC,∠ACB=90°,点D是BC边的中点,
∴CD⊥BC,∠A=∠DCB=45°,CD=![]() BC=AD,
BC=AD,
∴∠EAD=180°+45°=135°,∠ACD=180°-45°=135°,
又∵AE=CF,
∴△AED≌△CFD,
∴DE=DF,∠ADE=∠CDF,
又∵CD⊥BC,
∴∠ADE+∠ADF=∠CDF+∠ADF=∠CDA=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目


