题目内容
请阅读下列材料:
问题:如图1,在正方形ABCD和正方形CEFG中,点B、C、E在同一条直线上,M是线段AF的中点,连接DM,MG.探究线段DM与MG数量与位置有何关系.

小聪同学的思路是:延长DM交GF于H,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)直接写出上面问题中线段DM与MG数量与位置有何关系______;
(2)将图1中的正方形CEFG绕点C顺时针旋转,使正方形CEFG对角线CF恰好与正方形ABCD的边BC在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)如图3,将正方形CEFG绕点C顺时针旋转任意角度,原问题中的其他条件不变,写出你的猜想.
问题:如图1,在正方形ABCD和正方形CEFG中,点B、C、E在同一条直线上,M是线段AF的中点,连接DM,MG.探究线段DM与MG数量与位置有何关系.

小聪同学的思路是:延长DM交GF于H,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)直接写出上面问题中线段DM与MG数量与位置有何关系______;
(2)将图1中的正方形CEFG绕点C顺时针旋转,使正方形CEFG对角线CF恰好与正方形ABCD的边BC在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)如图3,将正方形CEFG绕点C顺时针旋转任意角度,原问题中的其他条件不变,写出你的猜想.
(1)如图1,在正方形ABCD和正方形CEFG中,AD∥BC∥GF,
∴∠DAM=∠HFM,
∵M是线段AF的中点,
∴AM=FM,
在△ADM和△FHM中,
,
∴△ADM≌△FHM(ASA),
∴DM=HM,AD=FH,
∵GD=CG-CD,GH=GF-FH,AD=CD,CG=GF,
∴GD=GH,
∴△DGH是等腰直角三角形,
∴DM=MG且DM⊥MG;
(2)如图2,延长DM交CF于H,连接GD,GH,
同(1)可得DM=HM,AD=FH,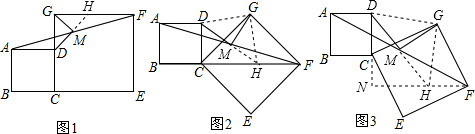
∵CF恰好与正方形ABCD的边BC在同一条直线上,
∴∠DCG=90°-45°=45°,
∠HFG=45°,
∴∠DCG=∠HFG,
在△CDG和△FHG中,
,
∴△CDG≌△FHG(SAS),
∴GD=GH,∠CGD=∠FGH,
∴∠DGH=∠CGD+∠CGH=∠FGH+∠CGH=∠CGF=90°,
∴△DGH是等腰直角三角形,
∴DM=MG且DM⊥MG;
(3)如图3,过点F作FH∥AD交DM的延长线于H,交DC的延长线于N,
同(1)可得DM=HM,AD=FH,
易得∠NCE=∠EFN,
∵∠DCG+∠NCE=180°-90°=90°,
∠HFG+∠EFN=90°,
∴∠DCG=∠HFG,
在△CDG和△FHG中,
,
∴△CDG≌△FHG(SAS),
∴GD=GH,∠CGD=∠FGH,
∴∠DGH=∠CGD+∠CGH=∠FGH+∠CGH=∠CGF=90°,
∴△DGH是等腰直角三角形,
∴DM=MG且DM⊥MG.
∴∠DAM=∠HFM,
∵M是线段AF的中点,
∴AM=FM,
在△ADM和△FHM中,
|
∴△ADM≌△FHM(ASA),
∴DM=HM,AD=FH,
∵GD=CG-CD,GH=GF-FH,AD=CD,CG=GF,
∴GD=GH,
∴△DGH是等腰直角三角形,
∴DM=MG且DM⊥MG;
(2)如图2,延长DM交CF于H,连接GD,GH,
同(1)可得DM=HM,AD=FH,

∵CF恰好与正方形ABCD的边BC在同一条直线上,
∴∠DCG=90°-45°=45°,
∠HFG=45°,
∴∠DCG=∠HFG,
在△CDG和△FHG中,
|
∴△CDG≌△FHG(SAS),
∴GD=GH,∠CGD=∠FGH,
∴∠DGH=∠CGD+∠CGH=∠FGH+∠CGH=∠CGF=90°,
∴△DGH是等腰直角三角形,
∴DM=MG且DM⊥MG;
(3)如图3,过点F作FH∥AD交DM的延长线于H,交DC的延长线于N,
同(1)可得DM=HM,AD=FH,
易得∠NCE=∠EFN,
∵∠DCG+∠NCE=180°-90°=90°,
∠HFG+∠EFN=90°,
∴∠DCG=∠HFG,
在△CDG和△FHG中,
|
∴△CDG≌△FHG(SAS),
∴GD=GH,∠CGD=∠FGH,
∴∠DGH=∠CGD+∠CGH=∠FGH+∠CGH=∠CGF=90°,
∴△DGH是等腰直角三角形,
∴DM=MG且DM⊥MG.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目


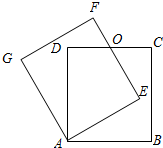 交且互相垂直,并说明这两条线段互相垂直的理由;
交且互相垂直,并说明这两条线段互相垂直的理由;