Question

如图，正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG，边EF与CD交于点O．
（1）以图中已标有字母的点为端点连接两条线段（正方形的对角线除外），要求所连接的两条线段相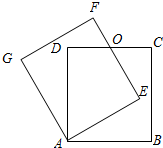交且互相垂直，并说明这两条线段互相垂直的理由；
（2）若正方形的边长为2cm，重叠部分（四边形AEOD）的面积为

4 3

3

cm2，求旋转的角度n．

Answer 1

（1）连接AO，AO⊥DE．
证明：∵在Rt△ADO与Rt△AEO中，AD=AE，AO=AO，
∴Rt△ADO≌Rt△AEO，
∴∠DAO=∠OAE（即AO平分∠DAE），
∴AO⊥DE（等腰三角形的三线合一）．

（2）n=30°．
理由：连接AO，
∵四边形AEOD的面积为

4 3

3

，
∴三角形ADO的面积

AD×DO

2

=

2 3

3

，
∵AD=2，
∴DO=

2 3

3

，在Rt△ADO中，∠DAO=30°，
∴∠EAD=60°，∠EAB=30°，
即n=30°．