题目内容
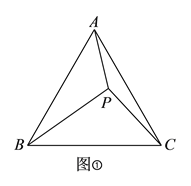
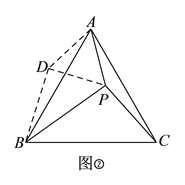
【题目】如图1是一个正三角形,分别连接这个正三角形各边上的中点得到图2,再连接图2中间的小三角形各边上的中点得到图3,按此方法继续下去.前三个图形中三角形的个数分别是1个,5个,9个,那么第5个图形中三角形的个数是个;第n个图形中三角形的个数是个.
【答案】17;4n﹣3
【解析】解:观察图形发现规律:后一个图形比前一个图形多4个三角形,
∵第一个图形中只有一个三角形,
∴第n个图形中有4(n﹣1)+1=4n﹣3个三角形.
令n=5,则4×5﹣3=17(个).
故答案为:17;4n﹣3.
(1)由已知图形可知:后一个图形比前一个图形多4个三角形,则第n个图形中的三角形有4(n-1)+1=4n-3个三角形。第5个图形中三角形的个数=4![]() 5-3=17,第第n个图形中三角形的个数为(4n-3)个。
5-3=17,第第n个图形中三角形的个数为(4n-3)个。

练习册系列答案
相关题目