Question

【题目】如图，一个凸六边形的六个内角都是120°，六条边的长分别为a，b，c，d，e，f，则下列等式中成立的是（ ）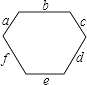

A.a+b+c=d+e+f
B.a+c+e=b+d+f
C.a+b=d+e
D.a+c=b+d

Answer 1

【答案】C
【解析】解：如图，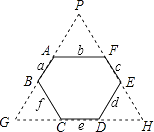

分别作直线AB、CD、EF的延长线和反向延长线使它们交于点G、H、P．
∵六边形ABCDEF的六个角都是120°，
∴六边形ABCDEF的每一个外角的度数都是60°．
∴△APF、△BGC、△DHE、△GHP都是等边三角形．
∴PA=PF=AF=b，BG=CG=BC=f，DH=EH=DE=d，
∴a+b+f=f+e+d=d+c+b，
∴a+b=e+d，f+e=c+b，a+f=d+c．
故答案为：C．
分别作线段AB、CD、EF的延长线和反向延长线使它们交于点G、H、P．根据已知条件可得△APF、△BGC、△DHE、△GHP都是等边三角形，所以有PA=PF=AF=b，BG=CG=BC=f，DH=EH=DE=d，PG=GH=PH,再结合线段的构成可知a+b+f=f+e+d=d+c+b，所以a+b=e+d，f+e=c+b，a+f=d+c．故选项C符合题意。