题目内容
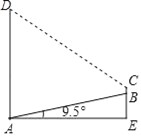
【题目】如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
(参考数据:sin19.5°≈![]() ,tan19.5°≈
,tan19.5°≈![]() ,最终结果精确到0.1m).
,最终结果精确到0.1m).
【答案】楼高AD为21.0米.
【解析】试题分析:(1)连接AC,由题意得![]() ,∠DAC=∠CAB,即可证明AE∥OC,从而得出∠OCE=90°,即可证得结论;
,∠DAC=∠CAB,即可证明AE∥OC,从而得出∠OCE=90°,即可证得结论;
(2)四边形AOCD为菱形.由![]() ,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形).
,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形).
试题解析:作CF⊥AD于点F.
在Rt△ABE中,∵AB=15,
∴BE=ABsin19.5°=15sin19.5°,
AE=ABcos19.5°=15cos19.5°,
在Rt△CDF中,∵CF=AE,∠DCF=45°,
∴DF=CF,
∴AD=DF+AF=CF+BC+BE=15cos19.5°+1.7+15sin19.5°≈21.0(m).
答:楼高AD为21.0米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目