题目内容
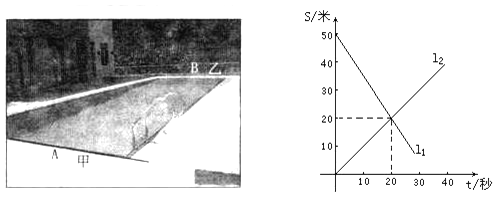
【题目】甲、乙两车分别从A地将一批物品运往B地，再返回A地，图6表示两车离A地的距离s（千米）随时间t（小时）变化的图象，已知乙车到达B地后以30千米/小时的速度返回．请根据图象中的数据回答：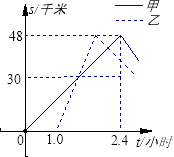
（1）甲车出发多长时间后被乙车追上？
（2）甲车与乙车在距离A地多远处迎面相遇？
（3）甲车从B地返回的速度多大时，才能比乙车先回到A地？
【答案】
（1）解：由图知，可设甲车由A地前往B地的函数解析式为s=kt，
将（2.4，48）代入，解得k=20，所以s=20t，
由图可知，在距A地30千米处，乙车追上甲车，所以当s=30千米时， 
（小时）即甲车出发1.5小时后被乙车追上
（2）解：由图知，可设乙车由A地前往B地函数的解析式为s=pt+m，
将（1.0，0）和（1.5，30）代入，得 
，解得 
，
所以s=60t﹣60，当乙车到达B地时，s=48千米．代入s=60t﹣60，得t=1.8小时，
又设乙车由B地返回A地的函数的解析式为s=﹣30t+n，
将（1.8，48）代入，得48=﹣30×1.8+n，解得n=102，
所以s=﹣30t+102，当甲车与乙车迎面相遇时，有﹣30t+102=20t
解得t=2.04小时代入s=20t，得s=40.8千米，即甲车与乙车在距离A地40.8千米处迎面相遇；
（3）解：当乙车返回到A地时，有﹣30t+102=0，解得t=3.4小时，
甲车要比乙车先回到A地，速度应大于 
（千米/小时）
【解析】（1）由图像可知，甲车由A地前往B地的函数是正比例函数，且图像过点（2.4，48），设函数解析式为s=kt，将点（2.4，48）代入解析式可求出k的值；根据图像的信息得，在距A地30千米处，乙车追上甲车，把s=30代入所求解析式即可求解。
（2）由图像可知，乙车由A地前往B地的函数是一次函数，且过点（1.0，0）和（1.5，30），设函数解析式为s=pt+m，将点（1.0，0）和（1.5，30）代入s=pt+m，得到关于p、m的方程组，解这个方程组即可求得p、m的值，即得乙车的解析式，当甲车与乙车迎面相遇时，两车的距离相等，于是可得关于t的方程pt+m=kt，再将求出的t的值代入所求的任意一个解析式中即可求出两车迎面相遇时与A地的距离。
（3）当乙车返回到A地时，乙车与A地的距离s=0，即pt+m=0，求出t的值，则乙车的速度可求，而甲车要比乙车先回到A地，那么甲车的速度只要大于乙车的速度即可。
