题目内容
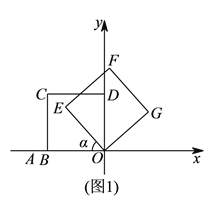
【题目】在平面直角坐标系中,点![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() .如图
.如图![]() ,正方形
,正方形![]() 的顶点
的顶点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在第二象限.现将正方形
在第二象限.现将正方形![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得到正方形
得到正方形![]() .
.

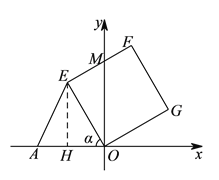
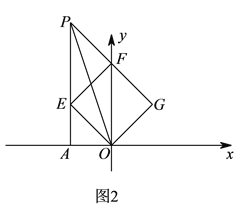
(![]() )如图
)如图![]() ,若
,若![]() ,
, ![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.
(![]() )若
)若![]() 为锐角,
为锐角, ![]() ,当
,当![]() 取得最小值时,求正方形
取得最小值时,求正方形![]() 的面积.
的面积.
(![]() )当正方形
)当正方形![]() 的顶点
的顶点![]() 落在
落在![]() 轴上时,直线
轴上时,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
, ![]() 的其中两边之比能否为
的其中两边之比能否为![]() ?若能,求出
?若能,求出![]() 的坐标;若不能,试说明理由.
的坐标;若不能,试说明理由.
【答案】(1)直线![]() 的函数表达式为
的函数表达式为![]() ;
;
(2)![]() ;
;
(3)能,点![]() 的坐标可为
的坐标可为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:(1)先判断出△AEO为正三角形,再根据锐角三角函数求出OM即可;(2)判断出当AE⊥OQ时,线段AE的长最小,用勾股定理计算即可;(3)由△OEP的其中两边之比为![]() :1分三种情况进行计算即可.
:1分三种情况进行计算即可.
试题解析:(![]() )过点
)过点![]() 作
作![]() 于点
于点![]() ,
, ![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() 为正三角形,
为正三角形,
∴![]() ,
, ![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,
![]() ,即
,即![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
把![]() 代入,
代入,
得![]() ,解得
,解得![]() ,
,
∴直线![]() 的函数表达式为
的函数表达式为![]() .
.
(![]() )当
)当![]() 时,线段
时,线段![]() 的长最小,
的长最小,
在![]() 中,
中,
![]() ,
,
即![]() ,
,
由勾股定理得![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() ,
,
此时, 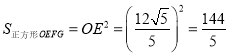 .
.
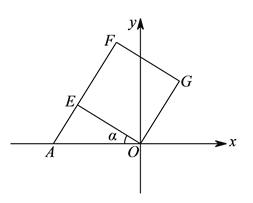
(![]() )能,
)能,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
①当![]() 与
与![]() 重合时,
重合时, ![]() 是等腰直角三角形(如图
是等腰直角三角形(如图![]() )
)
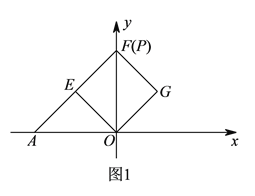
∴![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 坐标为
坐标为![]() .
.
当减小正方形的边长时,点![]() 在边
在边![]() 上,
上,
![]() 的其中两边之比不可能为
的其中两边之比不可能为![]() ,
,
当增加正方形的边长时,存在![]() (如图
(如图![]() )
)
和![]() (如图
(如图![]() )两种情况.
)两种情况.
②如图![]() 所示,当
所示,当![]() 时,
时,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,即
,即![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]() ,
,
![]() ,
,
即![]() .
.
![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
③如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 轴于点
轴于点![]() ,
,
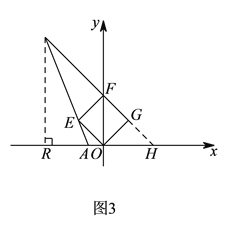
延长![]() 交
交![]() 轴于点
轴于点![]() .
.
∴![]() ,
,
![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
设正方形边长为![]() ,
, ![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
又∵![]() ,
,
![]() ,
,
在![]() 中,由勾股定理得,
中,由勾股定理得,
![]() ,即
,即![]() ,
,
∴![]() ,得
,得![]() ,
,
![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
即![]() ,
,
又∵在![]() 中,
中, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
则![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
④如图![]() 所示,当
所示,当![]() 与
与![]() 重合时,
重合时, ![]() 是等腰直角三角形,
是等腰直角三角形,
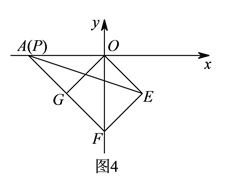
![]() ,
,
即![]() 满足条件,此时点
满足条件,此时点![]() 的坐标为
的坐标为![]() ,
,
在图![]() 的基础上,当正方形的边长减小时,
的基础上,当正方形的边长减小时,
![]() 的其中两边之比不可能为
的其中两边之比不可能为![]() ,
,
当正方形的边长增加时,存在![]() (图
(图![]() )
)
⑤如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 轴于点
轴于点![]() ,
,

记直线![]() 交
交![]() 轴于点
轴于点![]() ,
,
设正方形的边长为![]() ,
, ![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
∵![]() ,
,
![]() 即
即![]() ,
,
得![]() ,
,
![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,则
,则![]() ,
,
四边形![]() 是正方形,
是正方形,
∴![]() 即
即![]() ,
,
![]() 又
又![]() ,
,
∴![]() ,
,
![]() ,即
,即![]() ,
,
则![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,解得
,解得![]() ,
,
即![]() .
.
![]() 且
且![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,
,
综上所述,点![]() 的坐标可为
的坐标可为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

 作业辅导系列答案
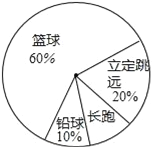
作业辅导系列答案【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;进球数的中位数为 个,众数为 个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).