题目内容
【题目】若△ABC和△DEF的面积分别为S1、S2 .
(1)如图①,AC=DF,BC=DE,∠C=30°,∠D=150°,比较S1与S2的大小为; 
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
(2)说明(1)的理由.
(3)如图②,在△ABC与△DEF中,AC=DF,BC=DE,∠C=30°,点E在以D为圆心,DE长为半径的半圆上运动,∠EDF的度数为α,比较S1与S2的大小(直接写出结果,不用说明理由). 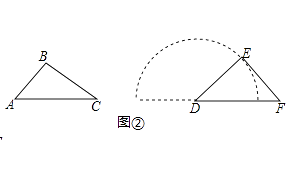
【答案】
(1)C
(2)解:如图1,

作BG⊥AC垂足为G,作EH⊥DF,垂足为H,
在Rt△BCG中,∠C=30°,
∴BG=BCsin∠C=BCsin30°= ![]() BC,
BC,
∴S1= ![]() AC×BG=
AC×BG= ![]() AC×
AC× ![]() BC=
BC= ![]() AC×BC
AC×BC
在Rt△EDH中,∠EDH=180°﹣∠EDF=30°,
∴EH=EDsin∠EDH=EDsin30°= ![]() ED,
ED,
∴S2= ![]() DF×EH=
DF×EH= ![]() DF×
DF× ![]() ED=
ED= ![]() DF×DE,
DF×DE,
∵BC=DE,AC=DF,
∴S1=S2
(3)解:如图2,过点B作BG⊥AC,
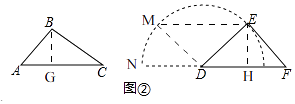
①当0°<α≤90°时,
在Rt△BCG中,∠C=30°,
∴BG=BCsin∠C=BCsin30°= ![]() BC,
BC,
∴S1= ![]() AC×BG=
AC×BG= ![]() AC×
AC× ![]() BC=
BC= ![]() AC×BC,
AC×BC,
∵BC=DE,AC=DF,
∴S1= ![]() DF×DE=
DF×DE= ![]() DF×DE×
DF×DE× ![]() ,
,
在Rt△EDH中,∠EDH=α,
∴EH=EDsin∠EDH=EDsinα,
∴S2= ![]() DF×EH=
DF×EH= ![]() DF×
DF× ![]() ED=
ED= ![]() DF×DEsinα,
DF×DEsinα,
Ⅰ、当sinα< ![]() 时,即:0°<α<30°时,S1>S2,
时,即:0°<α<30°时,S1>S2,
Ⅱ、当sinα= ![]() 时,即:α=30°时,S1=S2,
时,即:α=30°时,S1=S2,
Ⅲ、当sinα> ![]() 时,即:30°<α≤90°时,S1<S2,
时,即:30°<α≤90°时,S1<S2,
②当90°<α<180°时,设∠MDN=β=180°﹣α,
同①方法得,S1= ![]() DF×DE×
DF×DE× ![]() ,
,
S2= ![]() DF×DEsinβ,
DF×DEsinβ,
Ⅰ、当sinβ< ![]() 时,即:0°<β<30°时,
时,即:0°<β<30°时,
∴0°<180°﹣α<30°,即:150°<α<180°时,S1>S2,
Ⅱ、当sinβ= ![]() 时,即:β=30°时,即:α=150°时,S1=S2,
时,即:β=30°时,即:α=150°时,S1=S2,
Ⅲ、当sinβ> ![]() 时,即:30°<β<90°时,即:90°<α<150°时,S1<S2,
时,即:30°<β<90°时,即:90°<α<150°时,S1<S2,
综上所述,
Ⅰ.当α<30°、150°<α<180°时S1>S2;
Ⅱ.当α=30°、α=150°时S1=S2;
Ⅲ.当30°<α<150°时,S1<S2.
【解析】(1)先直接判断出结论,(2)用三角形的面积公式即可得出结论;(3)用三角形的面积公式,再用三角函数中正弦值的性质分类讨论即可得出结论.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案