题目内容
【题目】如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明. 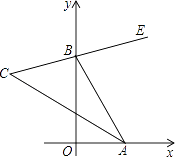
【答案】解:∠ACB的大小不发生改变, 如图,
∵BE平分∠ABF,CA平分∠OAB,
∴2∠EBA=∠ABF,∠OAB=2∠CAB,
又∵∠ABF为△AOB的外角,
∴∠ABF=∠AOB+∠OAB,
∵∠AOB=90°,
∴∠ABF=90°+∠OAB,
又∵∠EBA为△ACB的外角,
∴∠EBA=∠C+∠CAB,
∴90°+∠OAB=2(∠C+∠CAB),
90°+∠OAB=2∠C+∠OAB,
∴∠C=45°,
即∠ACB的大小不发生改变.
【解析】由BE平分∠ABF、CA平分∠OAB知2∠EBA=∠ABF、∠OAB=2∠CAB,根据△AOB外角性质得∠ABF=∠AOB+∠OAB,即∠ABF=90°+∠OAB,再根据△ACB外角性质得∠EBA=∠C+∠CAB,即90°+∠OAB=2(∠C+∠CAB),从而知90°+∠OAB=2∠C+∠OAB,即可得∠C=45°.
【考点精析】根据题目的已知条件,利用三角形的外角的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目