题目内容
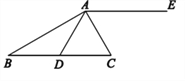
【题目】如图,在△ABC 中,点D 在B C 边上,BD=AD=AC,AC 平分∠DAE.
(1)设∠DAC=x°,将△ADC 绕点A 逆时针旋转x°,用直尺和圆规在图中画出旋转后的三角形,记点C 的对应点为C′;(保留作图痕迹)
(2)在(1)的条件下,若∠B=30°,证明四边形ADCC′是菱形.
【答案】(1)画图见解析;(2)证明见解析
【解析】试题分析:(1)在AE上截取AC′=AC,连接CC′即可;(2)通过证明四边相等来证明时菱形.
试题解析:
(1)如图所示.
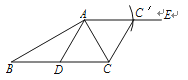
(2)证明: ∵ BD=AD,
∴ ∠B=∠BAD=30°.
∴ ∠ADC=∠B+∠BAD=60°.
∵ AD=AC,
∴ △ADC是等边三角形.
∴ AD=AC=DC.
由(1)得,A C′=AC,CC′=DC,
∴ AD=DC=CC′=A C′.
∴ 四边形ADCC′是菱形.

练习册系列答案
相关题目