题目内容
已知实数a,b,c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0.
(1)求a,b,c的值,并在平面直角坐标系中,描出点A(0,a),B(b,0),C(b,c)三点;
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示三角形POA的面积;
(3)在(2)的条件下,是否存在一点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
(1)求a,b,c的值,并在平面直角坐标系中,描出点A(0,a),B(b,0),C(b,c)三点;
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示三角形POA的面积;
(3)在(2)的条件下,是否存在一点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
(1)∵|a-2|+(b-3)2=0,(c-4)2≤0,
∴a-2=0,b-3=0,c-4=0,
∴a=2,b=3,c=4,
∴点A、B、C在平面直角坐标系中的位置如1图所示.
(2)如图2,过点P作PD⊥y轴,则PD=-m,
故三角形POA的面积=
OA•PD=
×2×(-m)=-m,即三角形POA的面积是-m;
(3)存在.理由如下:如图2,过点A做AE⊥BC于点E.则AE=3.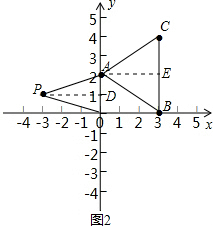
故△ABC的面积是6.
∵S四边形ABOP=S△AOB+S△AOP=3-m,
∴设存在点P使四边形ABOP的面积与△ABC的面积相等,即3-m=6,
解得m=-3,
∴P(-3,1).
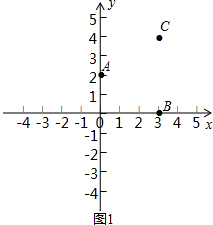
∴a-2=0,b-3=0,c-4=0,
∴a=2,b=3,c=4,
∴点A、B、C在平面直角坐标系中的位置如1图所示.
(2)如图2,过点P作PD⊥y轴,则PD=-m,
故三角形POA的面积=
| 1 |
| 2 |
| 1 |
| 2 |
(3)存在.理由如下:如图2,过点A做AE⊥BC于点E.则AE=3.
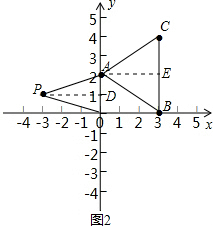
故△ABC的面积是6.
∵S四边形ABOP=S△AOB+S△AOP=3-m,
∴设存在点P使四边形ABOP的面积与△ABC的面积相等,即3-m=6,
解得m=-3,
∴P(-3,1).
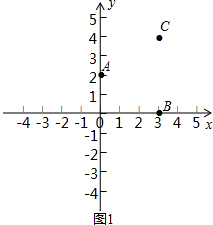

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目