题目内容
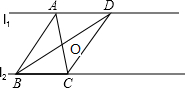
如图,已知△ABC,且S△ABC=1,D、E分别是AB、AC上的动点,BD与CE相交于点P,使SBCDE=
S△BPC,求S△DEP的最大值.

| 16 |
| 9 |

设S△BPC=9k,S△BPE=ak,S△DPC=bk,S△AED=x,
∵SBCDE=
S△BPC,
∴SBCDE=16k,
∵
=
=
=
,
∴S△DEP=
k,
∵S△DEP=S四边形EBCD-S△BPC-S△EBP-S△DPC=16k-9k-ak-bk,
∴
=7-a-b,
∵a+b≥2
,
∴
≤7-2
,
∴ab+18
-63≤0,
∴(
+21)(
-3)≤0,
∵
≥0,
∴0≤
≤3,
∴当a=b=3时,S△DEP最大值为k,
又∵
=
①,x+16k=1②,
由①②得:k=
,
∴S△DEP最大值为
.
∵SBCDE=
| 16 |
| 9 |
∴SBCDE=16k,
∵
| S△BPE |
| S△DPE |
| S△BPC |
| S△DPC |
| 9k |
| bk |
| 9 |
| b |
∴S△DEP=
| ab |
| 9 |
∵S△DEP=S四边形EBCD-S△BPC-S△EBP-S△DPC=16k-9k-ak-bk,
∴
| ab |
| 9 |
∵a+b≥2
| ab |
∴
| ab |
| 9 |
| ab |
∴ab+18
| ab |
∴(
| ab |
| ab |
∵
| ab |
∴0≤
| ab |
∴当a=b=3时,S△DEP最大值为k,
又∵
| x |
| 4k |
| x+4k |
| 12k |
由①②得:k=
| 1 |
| 18 |
∴S△DEP最大值为
| 1 |
| 18 |

练习册系列答案
相关题目