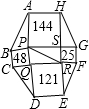
在平面直角坐标系中标出点A.O为坐标原点．连接OAB.求△OAB的面积．题目和参考答案——青夏教育精英家教网——

题目内容

在平面直角坐标系中标出点A（-2，3）、B（4，5），O为坐标原点．连接OAB，求△OAB的面积．

如图所示：
∵点A（-2，3）、B（4，5），
∴S_△OAB=S_梯形ABCD-S_△AOD-S_△BOC
=

1

2

（3+5）×6-

1

2

×2×3-

1

2

×4×5
=24-3-10
=11．

练习册系列答案

阳光考场单元测试卷系列答案

给力闯关100分系列答案

名校联盟冲刺卷系列答案

精英教程全能卷系列答案

课程达标冲刺100分系列答案

名校提分一卷通系列答案

百分金卷夺冠密题系列答案

微课堂百分大闯关系列答案

特级教师优化试卷系列答案

课程达标测试卷闯关100分系列答案

相关题目

已知D是△ABC边AB上的点，且△ABC的面积为2010，AD：DB=3：2，那么△ACD的面积是______．

如图，已知八边形ABCDEFGH中4个正方形的面积分别为25，144，48，121个平方单位，PR=13（单位），则该八边形的面积=______平方单位．

如图，直线l₁∥l₂，S_△ABC=24cm²，S_△OBC=14cm²，则S_△ODC=______cm²．

如图，将△ABC的三个顶点与同一个内点连接起来，所得三条连线把△ABC分成六个小三角形，其中四个小三角形面积在图中已标明，则△ABC的面积为______．

如图，△ABC是直角三角形，∠BAC=90°，AD、AE分别是△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm．
（1）求AD的长；
（2）求△AEC的面积．

已知A（0，2），点B（0，-3），点C在x轴上，如果△ABC的面积为20，求点C的坐标．

已知实数a，b，c满足关系式|a-2|+（b-3）²=0，（c-4）²≤0．
（1）求a，b，c的值，并在平面直角坐标系中，描出点A（0，a），B（b，0），C（b，c）三点；
（2）如果在第二象限内有一点P（m，1），请用含m的式子表示三角形POA的面积；
（3）在（2）的条件下，是否存在一点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．

如图，△ABC为等腰直角三角形，D为AB中点，AB=2，扇形ADG和BDH分别是以A，B为圆心，AD，BD为半径的圆的

，则阴影部分面积为______．