题目内容
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: ![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
【答案】①证明:连接AC,BE,作直线OC,如图所示: 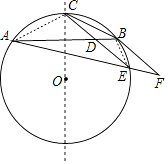
∵BE=EF,
∴∠F=∠EBF;
∵∠AEB=∠EBF+∠F,
∴∠F= ![]() ∠AEB,
∠AEB,
∵C是 ![]() 的中点,∴
的中点,∴ ![]() ,
,
∴∠AEC=∠BEC,
∵∠AEB=∠AEC+∠BEC,
∴∠AEC= ![]() ∠AEB,
∠AEB,
∴∠AEC=∠F,
∴CE∥BF;
②解:∵∠DAE=∠DCB,∠AED=∠CEB,
∴△ADE∽△CBE,
∴ ![]() ,即
,即 ![]() ,
,
∵∠CBD=∠CEB,∠BCD=∠ECB,
∴△CBE∽△CDB,
∴ ![]() ,即
,即 ![]() ,
,
∴CB=2 ![]() ,
,
∴AD=6,
∴AB=8,
∵点C为劣弧AB的中点,
∴OC⊥AB,AG=BG= ![]() AB=4,
AB=4,
∴CG= ![]() =2,
=2,
∴△BCD的面积= ![]() BDCG=
BDCG= ![]() ×2×2=2.
×2×2=2.
【解析】①连接AC,BE,由等腰三角形的性质和三角形的外角性质得出∠F= ![]() ∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;②证明△ADE∽△CBE,得出
∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;②证明△ADE∽△CBE,得出 ![]() ,证明△CBE∽△CDB,得出
,证明△CBE∽△CDB,得出 ![]() ,求出CB=2
,求出CB=2 ![]() ,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG=
,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG= ![]() AB=4,由勾股定理求出CG=
AB=4,由勾股定理求出CG= ![]() =2,即可得出△BCD的面积.
=2,即可得出△BCD的面积.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):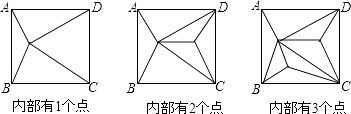
(1)填写如表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)