��Ŀ����
����Ŀ����ͼ��������ABCD�ڲ������ɸ��㣬����Щ���Լ�������ABCD�Ķ���A��B��C��D��ԭ�����ηָ��һЩ�����Σ�����ص�����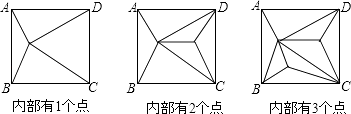
��1��������
������ABCD�ڵ�ĸ��� | 1 | 2 | 3 | 4 | �� | n |
�ָ�ɵ������εĸ��� | 4 | 6 | �� |
��2�����ԭ�����α��ָ��2016�������Σ���ʱ������ABCD�ڲ��ж��ٸ��㣿
��3�����������£����������ָܷ��2017�������Σ����ܣ���ʱ������ABCD�ڲ��ж��ٸ��㣿�����ܣ���˵�����ɣ�
��4�����Ͻ��ۣ�����ʲô���֣���д��һ�����ɣ�
���𰸡�
��1��8��10��2��n+1��
��2��
�⣺�����Ϊn��
��2��n+1��=2016��
���n=1007��
��ԭ�����α��ָ��2016��������ʱ������ABCD�ڲ���1007���㣮
��3��
�⣺�����Ϊn��
��2��n+1��=2017��
���n=1007.5��
��ԭ�����β����ָ��2017�������Σ�
��4��
�⣺���ָ�ɵ������εĸ�����Զ��ż������
����������1������ͼ���ص��ҳ�������ABCD�ڵ�ĸ�����ָ�ɵ������εĸ����Ĺ�ϵ���ܽ���ɼ��ɣ���2�����ݹ����г����̣��ⷽ�̵õ��𰸣���3���г����������������У������У���4���������ɣ�

����Ŀ��������Զ��С��ͬѧ�����п���ѡ����Ŀ֮һ��ij���������ϣ�������ʦ��¼��С�յ�һ��������Զѵ���ɼ����±���
�ɼ���m�� | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
���� | 1 | 1 | 2 | 5 | 1 |
�����й����������ݵ�˵������ȷ���ǣ� ��
A.������2.45
B.ƽ������2.45
C.�����2.5
D.������0.48