题目内容
【题目】![]() 是⊙
是⊙![]() 的内接三角形,
的内接三角形, ![]() .⊙
.⊙![]() 的半径为
的半径为![]() ,
, ![]() 到
到![]() 的距离为
的距离为![]() .
.
(![]() )求
)求![]() 的长;
的长;
(![]() )
)![]() 的度数为__________.
的度数为__________.
【答案】(1)![]() ;(2)60°或120°.
;(2)60°或120°.
【解析】试题分析:(1)分两种情况考虑:当三角形ABC为锐角三角形时,过A作AD垂直于BC,根据题意得到AD过圆心O,连接OB,在直角三角形OBD中,由OB与OD长,利用勾股定理求出BD的长,进而可求出BC的长;当三角形ABC为钝角三角形时,同理求出BC的长即可;
(2)根据(1)中的数据分别计算即可求出BAC的度数.
试题解析:(1)分两种情况考虑:
当△ABC为锐角三角形时,如图1所示,
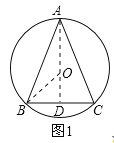
过A作AD⊥BC,由题意得到AD过圆心O,连接OB,
∵OD=1,OB=2,
∴在Rt△OBD中,根据勾股定理得:BD=![]() ,
,
∴BC=2BD=2![]() ;
;
当△ABC为钝角三角形时,如图2所示,
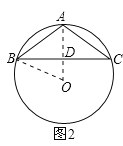
过A作AD⊥BC,由题意得到AD延长线过圆心O,连接OB,
∵OD=1,OB=2,
∴在Rt△OBD中,根据勾股定理得:BD=![]() ,
,
∴BC=2BD=2![]() ;
;
(2)图1中,
∵OD=1,OB=2,
∴∠OBD=30°,
∴∠BOD=60°,
∴∠BAC=60°;
图2中,∵OD=1,OB=2,
∴∠OBD=30°,
∴∠ACB=30°,
∵AB=AC,
∴∠BAC=120°.
故∠BAC的度数为60°或120°.

练习册系列答案
相关题目





