Question

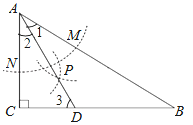
【题目】如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（ ）.

①作出AD的依据是SAS；②∠ADC=60°

③点D在AB的中垂线上；④S△DAC：S△ABD=1：2．

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

①根据作图的过程可以判定作出AD的依据；

②利用角平分线的定义可以推知∠CAD=30°，则由直角三角形的性质来求∠ADC的度数；

③利用等角对等边可以证得△ADB的等腰三角形，由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上；

④利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比．

解：①根据作图的过程可知，作出AD的依据是SSS；

故①错误；

②如图，∵在△ABC中，∠C=90°，∠B=30°，

∴∠CAB=60°．

又∵AD是∠BAC的平分线，

∴∠1=∠2=∠CAB=30°，

∴∠3=90°﹣∠2=60°，即∠ADC=60°．

故②正确；

③∵∠1=∠B=30°，

∴AD=BD，

∴点D在AB的中垂线上．

故③正确；

④∵如图，在直角△ACD中，∠2=30°，

∴AD=2CD，

∴BD=2CD，

∵S△DAC=ACCD，S△ABD=ACBD，

∴S△DAC：S△ABD=ACCD：ACBD =CD：BD=1：2，

即S△DAC：S△ABD=1：2．

故④正确．

综上所述，正确的结论是：②③④，共有3个．

故选C．