Question

【题目】如图，在中， 为边的中点． 是上一点，⊙与相切于点，且与、分别相交于点、．连接交于点．

（）求证： ．

（）已知， ．当是⊙的直径时，求的长．

Answer 1

【答案】见解析

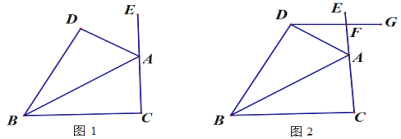
【解析】试题分析：（1）如图1中，作OM⊥AB于M，ON⊥AC于N，连接OE、OF，首先证明OM=ON，△OEM≌△OFN，只要证明EF⊥AD，BC⊥AD即可证明．

（2）如图2中，设OE=OF=OD=x，由EF∥BC，得，列出方程即可解决问题．

试题解析：（）证明：如图，作于， 于，连、，

∵与相切于点，∴，

∵在中， 为的中点，

∴为的中垂线，得，

∴等腰中， 平分， ，

∵， ，

∴，

在和中，

，

∴≌，

∴，

∵， ，

∴，

∴平分，

又∵，

∴在等腰中， ，

∵， 在上，

∴，

（）如图，设，

在中， ， ， ，

∴，

由（）得， ，

∴，

∴，

解得，

∴．