题目内容
【题目】在平面直角坐标系中，抛物线
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C.
（1）求点A的坐标；
（2）当S△ABC=15时，求该抛物线的表达式；
（3）在（2）的条件下，经过点C的直线
与抛物线的另一个交点为D.该抛物线在直线
上方的部分与线段CD组成一个新函数的图象。请结合图象回答：若新函数的最小值大于﹣8，求k的取值范围.
【答案】（1）（﹣1，0）；（2）y=x2﹣4x﹣5；（3）当﹣1＜k＜0时新函数的最小值大于﹣8．
【解析】试题分析：（1）对于抛物线解析式，令y=0得到关于x的方程，求出方程的解，根据A在B的左侧且m大于0，求A的坐标即可；
（2）由（1）的结果表示出B的坐标，根据抛物线与y轴交于点C，表示出C坐标，进而表示出AB与OC，由三角形ABC面积为15，利用三角形面积公式列出关于m的方程，求出方程的解得到m的值，即可确定出抛物线解析式；
（3）由（2）中m的值确定出C坐标，设直线l解析式为y=kx+b，把C坐标代入求出b的值，抛物线解析式配方后，经判断得到当点D在抛物线对称轴右侧时，新函数的最小值有可能大于-8，令y=-8求出x的值，确定出抛物线经过点（3，-8），把（3，-8）代入一次函数解析式求出k的值，由图象确定出满足题意k的范围即可．
试题解析：（1）∵抛物线y=x2﹣（m﹣1）x﹣m（m＞0）与x轴交于A、B两点，
∴令y=0，即x2﹣（m﹣1）x﹣m=0，
解得：x1=﹣1，x2=m，
又∵点A在点B左侧，且m＞0，
∴点A的坐标为（﹣1，0）；
（2）由（1）可知点B的坐标为（m，0），
∵抛物线与y轴交于点C，
∴点C的坐标为（0，﹣m），
∵m＞0，
∴AB=m+1，OC=m，
∵S△ABC=15，
∴
m（m+1）=15，即m2+m﹣30=0，
解得：m=﹣6或m=5，
∵m＞0，
∴m=5；
则抛物线的表达式为y=x2﹣4x﹣5；
（3）由（2）可知点C的坐标为（0，﹣5），
∵直线l：y=kx+b（k＜0）经过点C，
∴b=﹣5，
∴直线l的解析式为y=kx﹣5（k＜0），
∵y=x2﹣4x﹣5=（x﹣2）2﹣9，
∴当点D在抛物线顶点处或对称轴左侧时，新函数的最小值为﹣9，不符合题意；
当点D在抛物线对称轴右侧时，新函数的最小值有可能大于﹣8，
令y=﹣8，即x2﹣4x﹣5=﹣8，
解得：x1=1（不合题意，舍去），x2=3，
∴抛物线经过点（3，﹣8），
当直线y=kx﹣5（k＜0）经过点（3，﹣8）时，可求得k=﹣1，
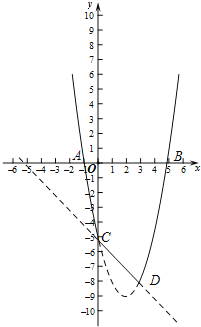
由图象可知，当﹣1＜k＜0时新函数的最小值大于﹣8．
