题目内容
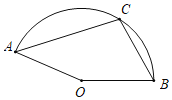
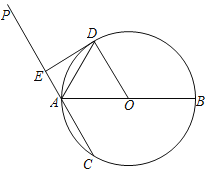
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
【答案】(1)ED为⊙O的切线,见解析;(2)6
【解析】
(1)连接AD,根据角平分线的定义得到∠DAE=∠DAO,得到∠ODA=∠DAE,根据平行线的性质得到OD⊥DE,于是得到结论;
(2)过O作OH⊥PC,则四边形EHOD是矩形,求得OH=DE,EH=OD,设AE=x,则DE=2x,根据勾股定理列方程即可得到结论.
解:(1)连接AD,∵AD平分∠PAB,
∴∠DAE=∠DAO,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AE,
∴OD⊥DE,
∴ED为⊙O的切线;
(2)过O作OH⊥PC,
则四边形EHOD是矩形,
∴OH=DE,EH=OD,
∵AB=10,
∴EH=OD=5,
∵ED=2AE,
∴设AE=x,则DE=2x,
∴AH=5﹣x,OH=2x,
∵OA2=AH2+OH2,
∴52=(5﹣x)2+(2x)2,
解得:x=2,x=0(不合题意舍去),
∴AE=2,AH=3,
∴AC=6.

练习册系列答案
相关题目