题目内容
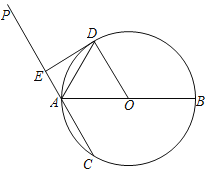
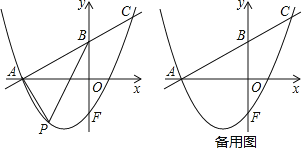
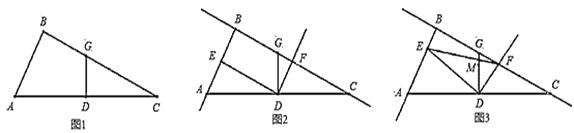
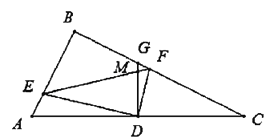
【题目】已知，如图1，在
中，
，
，
，若
为
的中点，
交
与点
.
（1）求
的长.
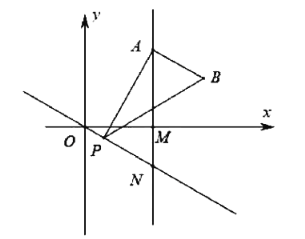
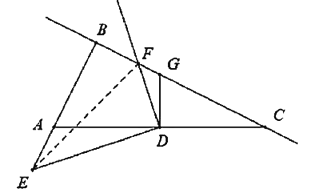
（2）如图2，
点为射线
上一动点，连接
，线段绕点顺时针旋转
交直线与点
.
①若
时，求
的长：
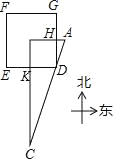
②如图3，连接
交直线
与点
，当
为等腰三角形时，求
的长.
【答案】（1）
；（2）①
，
； ②
，
.
【解析】
（1）先利用相似三角形性质求得
∽
，并利用相似比即可求
的长；
（2）①由题意分点
在线段
上，点在射线
上，利用相似三角形性质进行分析求值；
②利用三角函数以及等腰三角形性质综合进行分析讨论.
解：（1）∵
，
，
∴∽
∴
∵
，
∴
∴
（2）①（
）点在线段上
∵
，
∴为的中点
∵
为
的中点
∴
∵，
∴
∴
是的中位线
∴
（
）点在射线上
∵为的中点，
∴
由（1）可得
∽
∴
，
∴
∵
，
∴
∴
∽
∴
∴
综上所述：
的长为，
②由上问可得，∽
∴
∵
∴
∵，
∴
∴
∽
为等腰三角形，则为等腰三角形.
（）
时
在延长线上，不符合题意，舍去
（）
（
）
，
则点
与点
重合
综上所述：
的长为，
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
