题目内容
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于点C(0,﹣3).
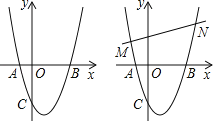
(1)求二次函数解析式;
(2)若点Q为抛物线上一点,且S△ABQ=![]() S△ACQ,求点Q的坐标;
S△ACQ,求点Q的坐标;
(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若![]() =5,求m的值.
=5,求m的值.
【答案】(1)y=x2﹣2x﹣3;(2)点Q的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );(3)m=±2.
);(3)m=±2.
【解析】
(1)抛物线与y轴交于点C(0,-3),则c=-3,将点B的坐标代入抛物线表达式并解得:b=-2,即可求解;
(2)分点Q在x轴下方、点Q在x轴上方两种情况,分别求解即可;
(3)MH=![]() (t-x1),同理:NH=(x2-t)
(t-x1),同理:NH=(x2-t)![]() ,MHMN=(m2+1)(mt+n-t2+2t+3)=(m2+1)PH,即可求解.
,MHMN=(m2+1)(mt+n-t2+2t+3)=(m2+1)PH,即可求解.
解:(1)抛物线与y轴交于点C(0,﹣3),则c=﹣3,
将点B的坐标代入抛物线表达式并解得:b=﹣2,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)设:点Q(m,m2﹣2m﹣3),
①当点Q在x轴下方时,如图1,
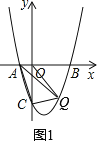
S△ACQ=![]() ×4×(﹣m2+2m+3),
×4×(﹣m2+2m+3),
S△ABQ=S△AOC+S△QOC﹣S△AOQ=![]() ﹣
﹣![]() ×3×m﹣
×3×m﹣![]() ×1×(﹣m2+2m+3)=
×1×(﹣m2+2m+3)=![]() m2+
m2+![]() m,
m,
则:![]() ×4×(﹣m2+2m+3)=
×4×(﹣m2+2m+3)=![]() m2+
m2+![]() m,
m,
解得:m=![]() 或﹣1(舍去﹣1),故点P(
或﹣1(舍去﹣1),故点P(,﹣
![]() );
);
②当点Q在x轴上方时,如图2,
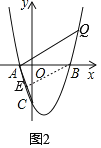
取AC的中点E(﹣![]() ,﹣
,﹣![]() ),
),
S△ABQ=![]() S△ACQ,则点E、B到AQ的距离相等,BE∥AQ,
S△ACQ,则点E、B到AQ的距离相等,BE∥AQ,
直线BE的表达式中的k值为:![]() ,
,
同理直线BQ的表达式为:y=![]() x+
x+![]() ,
,
∴ ,
,
解得:x=![]() 或﹣1(舍去﹣1),
或﹣1(舍去﹣1),
故点Q(![]() ,
,![]() );
);
综上,点Q的坐标为:(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );
);
(3)过点H作x轴的平行线RH,过点M、N分别作RH的垂线交于点R、S,
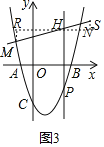
设点M、N的横坐标分别为x1,x2,点P(t,t2﹣2t﹣3),则点H(m,mt+n),
则PH=mt+n﹣t2+2t+3,
联立直线与抛物线的表达式并整理得:
x2﹣(m+2)x﹣3﹣n=0,
则x1+x2=m+2,x1x2=﹣3﹣n
直线M、N的k值为m,即tan∠RHM=m=tanα,则cosα=![]() ,
,
∴MH=![]() (t﹣x1),同理:NH=(x2﹣t)
(t﹣x1),同理:NH=(x2﹣t)![]() ,
,
∴MHMN=(m2+1)(mt+n﹣t2+2t+3)=(m2+1)PH,
而![]() ,则m2+1=5,
,则m2+1=5,
解得:m=±2.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
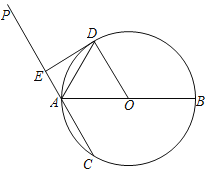
智趣暑假温故知新系列答案【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
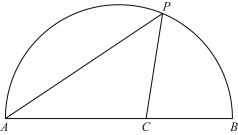
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).