题目内容
【题目】在平面直角坐标系xOy中,抛物线![]() 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线![]() 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
【答案】(1)顶点D(m,1-m);(2)向左平移了1个单位,向上平移了2个单位;(3)m=-1或m=-2.
【解析】试题分析: ![]() 把抛物线的方程配成顶点式,即可求得顶点坐标.
把抛物线的方程配成顶点式,即可求得顶点坐标.
![]() 把点
把点![]() 代入求出抛物线方程,根据平移规律,即可求解.
代入求出抛物线方程,根据平移规律,即可求解.
![]() 分两种情况进行讨论.
分两种情况进行讨论.
试题解析:(1)∵![]() ,
,
∴顶点D(m,1-m).
(2)∵抛物线![]() 过点(1,-2),
过点(1,-2),
∴![]() .
.
即![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴抛物线的顶点是(2,-1).
∵抛物线![]() 的顶点是(1,1),∴向左平移了1个单位,向上平移了2个单位.
的顶点是(1,1),∴向左平移了1个单位,向上平移了2个单位.
(3)∵顶点D在第二象限,∴![]() .
.
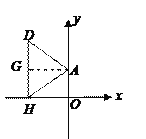
情况1,点A在![]() 轴的正半轴上,如图(1).作
轴的正半轴上,如图(1).作![]() 于点G,
于点G,
∵A(0, ![]() ),D(m,-m+1),
),D(m,-m+1),
∴H(![]() ),G(
),G(![]() ),
),
![]()
∴![]() .∴
.∴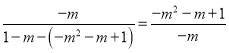 .
.
整理得: ![]() .∴
.∴![]() 或
或![]() (舍).
(舍).
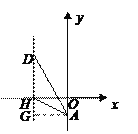
情况2,点A在![]() 轴的负半轴上,如图(2).作
轴的负半轴上,如图(2).作![]() 于点G,
于点G,
∵A(0, ![]() ),D(m,-m+1),∴H(
),D(m,-m+1),∴H(![]() ),G(
),G(![]() ),
),
![]()
∴![]() .∴
.∴ .
.
整理得: ![]() .∴
.∴![]() 或
或![]() (舍),
(舍),
![]() 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目