题目内容
如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D.若CD=CF,则 .
.

 .
.
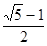 .
.试题分析:由题中条件可得Rt△AFB∽Rt△ABC,设CF=m,AF=n,根据相似三角形的对应边成比例可得m、n之间的关系,再由Rt△AFE∽Rt△CFB,即可得出AE与AD的关系.
如图,设CF=m,AF=n,
∵AB⊥BC,BF⊥AC,
∴∠ABF+∠CBF=90°,∠ABF+∠BAF=90°,
∴∠CBF=∠BAF,又∠ABC=∠BFC=90°,
∴Rt△AFB∽Rt△ABC,
∴AB2=AF?AC,又FC=CD=AB=m,
∴m2=n(n+m),
即

∴
 (舍去)
(舍去)又Rt△AFE∽Rt△CFB,

即
 .
.
练习册系列答案
相关题目
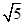 ,sinB=
,sinB=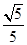 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.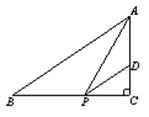
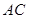 、
、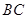 的长;
的长;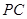 的长为
的长为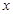 ,
,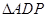 的面积为
的面积为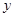 .当
.当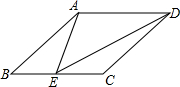
 和△
和△ 中,
中, ,
,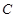 为线段
为线段 上一点,且
上一点,且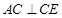 .
. .
.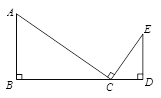


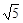
 DC.则图中阴影部分面积为 .
DC.则图中阴影部分面积为 .

 处,
处,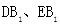 分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为( ).
分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为( ).
 中,点D、E分别在边AB 、AC上,下列比例式不能判定
中,点D、E分别在边AB 、AC上,下列比例式不能判定 ∥
∥ 的是( ).
的是( ).
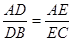 ; B.
; B.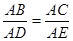 ;C.
;C. ;D.
;D. .
.