题目内容
如图,在面积为24的菱形ABCD中,E、F分别是边AD、BC的中点,点G、H在DC边上,且GH = DC.则图中阴影部分面积为 .
DC.则图中阴影部分面积为 .

 DC.则图中阴影部分面积为 .
DC.则图中阴影部分面积为 .
7.
试题分析:连接EF、EH、GF,判断出四边形EFCD是平行四边形,SEFCG=12,结合
 ,可分别得出S△HOG=s,则S△EFO=4s,S△EOH=2s,S△OFG=2s,从而求出s的值,代入即可得出阴影部分的面积:
,可分别得出S△HOG=s,则S△EFO=4s,S△EOH=2s,S△OFG=2s,从而求出s的值,代入即可得出阴影部分的面积:如图,连接EF、EH、GF,则四边形EFCD是平行四边形,SEFCG=12,
由题意得,
 ,
,设S△HOG=s,则S△EFO=4s,S△EOH=2s,S△OFG=2s,
∵HG=DH+CG,∴S△EHG=S△EDH+S△FCG=3s,
综上可得:S△EDH+S△FCG+S△HOG+S△EFO+S△OFG+S△EOH=12,即12s=12,解得:s=1,
∴阴影部分的面积为:7s=7.


练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 DC,连结
DC,连结 并延长交
并延长交 的延长线于点
的延长线于点




 ,则△EFC的周长为( )
,则△EFC的周长为( )





 .
.

 是线段
是线段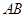 的黄金分割点,
的黄金分割点, >
> ,且
,且 ,则
,则 .
.