题目内容
【题目】如图,在平面直角坐标系中,直线y=﹣![]() 分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
(1)填空:b= ;
(2)点D的坐标为 ;
(3)点M是线段AB上的一个动点(点A、B除外),在x轴上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
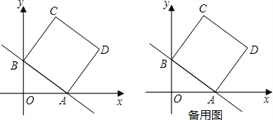
【答案】(1)b=6;
(2)点D的坐标为(14,8);
(3)存在,x轴上方的点N有两个,分别为(![]() ,
, ![]() )和(﹣4,3).
)和(﹣4,3).
【解析】(1)把(4,0)代入y=![]() x+b即可求得b的值;
x+b即可求得b的值;
(2)过点D作DE⊥x轴于点E,证明△OAB≌△EDA,即可求得AE和DE的长,则D的坐标即可求得;
(3)分当OM=MB=BN=NO时;当OB=BN=NM=MO=3时两种情况进行讨论.
解:∵直线y=![]() x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),
x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),
∴![]() ﹣×8+b=0,
﹣×8+b=0,
解得:b=6,;
(2)如图1,过点D作DE⊥x轴于点E,
则∠AOB=∠DEA=90°,
∴∠1+∠2=90°,∠2+∠3=90,
∴∠1=∠3,
又∵四边形ABCD是正方形,
∴AB=DA,
∵在△AOB和△DEA中,
∠1=∠3,∠AOB=∠DEA=90°,AB=DA,
∴△AOB≌△DEA(AAS),
∴OA=DE=8,OB=AE=6,
∴OE=OA+AE=8+6=14,
∴点D的坐标为(14,8);
(3)存在.
①如图2,当OM=MB=BN=NO时,四边形OMBN为菱形.连接NM,交OB于点P,则NM与OB互相垂直平分,
∴OP=![]() OB=3,
OB=3,
∴当y=3时, ![]() x+6=3,
x+6=3,
解得:x=4,
∴点M的坐标为(4,3),
∴点N的坐标为(﹣4,3).
②如图3,当OB=BN=NM=MO=6时,四边形BOMN为菱形.延长NM交x轴于点P,则MP⊥x轴.
∵点M在直线y=![]() x+6上,
x+6上,
∴设点M的坐标为(a, ![]() a+6)(a>0),
a+6)(a>0),
在Rt△OPM中,OP2+PM2=OM2,
即:a2+(![]() a+6)2=62,
a+6)2=62,
整理得: ![]() a2﹣9a=0,
a2﹣9a=0,
∵a>0,
∴![]() a﹣9=0,
a﹣9=0,
解得:a=![]() ,
,
∴点M的坐标为(![]() ,
, ![]() ),
),
∴点N的坐标为(![]() ,
, ![]() ).
).
综上所述,x轴上方的点N有两个,分别为(![]() ,
, ![]() )和(﹣4,3).
)和(﹣4,3).

“点睛”此题考查了待定系数法求函数解析式、全等三角形的判定与性质、正方形的性质、菱形的性质、勾股定理以及一元二次方程,主要掌握方程思想、分类讨论思想与数形结合思想的应用.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 68 | 109 | 136 | 345 | 368 | 701 |
摸到乒乓球的频率 | 0.68 | 0.73 | 0.68 | 0.69 | 0.70 | 0.70 |
(1)请估计:当n很大时,摸到白球的频率将会接近________;
(2)假如你去摸一次,你摸到白球的概率是_______,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?