题目内容
【题目】如图，将
ABCD的边AB延长到点E，使BE＝AB，连接DE，交边BC于点F．
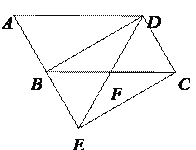
（1）求证：△BEF≌△CDF．
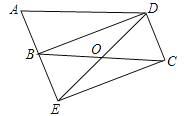
（2）连接BD，CE，若∠BFD＝2∠A，求证四边形BECD是矩形．
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据平行四边形的判定与性质得到四边形BECD为平行四边形，然后由SSS推出两三角形全等即可；
（2）要证明四边形BECD是矩形，只需推知BC=ED．
试题解析：（1）在平行四边形ABCD中，AD=BC，AB=CD，AB∥CD，则BE∥CD，又∵AB=BE，∴BE=DC，∴四边形BECD为平行四边形，∴BD=EC，在△ABD与△BEC中，∵AB=BE，BD=EC，AD=BC，∴△ABD≌△BEC（SSS）；
（2）由（1）知，四边形BECD为平行四边形，则OD=OE，OC=OB．∵四边形ABCD为平行四边形，∴∠A=∠BCD，即∠A=∠OCD，又∵∠BOD=2∠A，∠BOD=∠OCD+∠ODC，∴∠OCD=∠ODC，∴OC=OD，∴OC+OB=OD+OE，即BC=ED，∴平行四边形BECD为矩形．
练习册系列答案
名校课堂系列答案
相关题目
