��Ŀ����
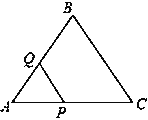
����Ŀ����ͼ�ֱ���ֱ��������ABC����Ϊ�����������������Σ�������ֱ���S1��S2��S3��ʾ������֤��S1=S2��S3��
��1����ͼ�ֱ���ֱ��������ABC����Ϊֱ��������������Բ��������ֱ���S1��S2��S3��ʾ����BC=a��AC=b��AB=c������ȷ��S1��S2��S3֮��Ĺ�ϵ��֤����
��2����ͼ�ֱ���ֱ��������ABC����Ϊ�������������������Σ�������ֱ���S1��S2��S3��ʾ������ȷ��S1��S2��S3֮��Ĺ�ϵ��������֤����
��3�����ֱ���ֱ��������ABC����Ϊ������������������Σ�������ֱ���S1��S2��S3��ʾ���������S1��S2��S3֮��Ĺ�ϵ��������֤����

���𰸡���1����1��S1=S2+S3��֤����������
��2��S1=S2+S3��
��3��S1=S2+S3
�������������������1����ͼ1�Ĺ��ɿɵ�S1=S2+S3��
��2�����ݹ��ɶ�����õȱ������εĸߣ������������ɵ�S1=S2+S3��
��3�����������������ε�����ȵ������Ʊȵ�ƽ�����ɵ�![]() ��
�� ![]() ����
����![]() ����S1=S2+S3��
����S1=S2+S3��
�����������1����Rt��ABC����BC��CA��AB�ij��ֱ�Ϊa��b��c����c2=a2+b2��
��S1=S2+S3
��2��S1=S2+S3��֤�����£�
��ȻS1=![]() c2��S2=
c2��S2=![]() a2��S3=
a2��S3=![]() b2��
b2��
��S2+S3=![]() ��a2+b2��=
��a2+b2��=![]() c2=S1��
c2=S1��
��3������������������������ʱ��S1=S2+S3��
�������������������ƣ�
��![]() ��
�� ![]() ��
��
��![]() ��
��
��S1=S2+S3��
����������ABC�������ƶ���Σ�S1=S2+S3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�