题目内容
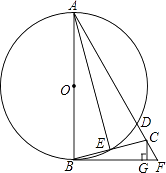
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) 
A.π
B.π+5
C.![]()
D.![]()
【答案】D
【解析】解:作DH⊥AE于H, ∵∠AOB=90°,OA=2,OB=1,
∴AB= ![]() =
= ![]() ,
,
由旋转的性质可知,OE=OB=1,DE=EF=AB= ![]() ,△DHE≌△BOA,
,△DHE≌△BOA,
∴DH=OB=1,
阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积
= ![]() ×3×1+
×3×1+ ![]() ×1×2+
×1×2+ ![]() ﹣
﹣ ![]()
= ![]() ﹣
﹣ ![]() π,
π,
故选:D.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2),以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?