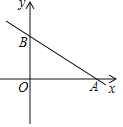题目内容
【题目】如图，抛物线y=ax2+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．
（1）求抛物线的解析式，并求出点B坐标；
（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）
（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD相似？若存在请求出P点的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵点A（1，0）和点C（0，1）在抛物线y=ax2+b上，
∴ 
，解得：a=﹣1，b=1，
∴抛物线的解析式为：y=﹣x2+1，
抛物线的对称轴为y轴，则点B与点A（1，0）关于y轴对称，∴B（﹣1，0）
（2）
解：设过点A（1，0），C（0，1）的直线解析式为y=kx+b，可得：
，解得k=﹣1，b=1，∴y=﹣x+1．
∵BD∥CA，∴可设直线BD的解析式为y=﹣x+n，
∵点B（﹣1，0）在直线BD上，∴0=1+n，得n=﹣1，
∴直线BD的解析式为：y=﹣x﹣1．
将y=﹣x﹣1代入抛物线的解析式，得：﹣x﹣1=﹣x2+1，解得：x1=2，x2=﹣1，
∵B点横坐标为﹣1，则D点横坐标为2，
D点纵坐标为y=﹣2﹣1=﹣3，∴D点坐标为（2，﹣3）．
如答图①所示，过点D作DN⊥x轴于点N，则DN=3，AN=1，BN=3，
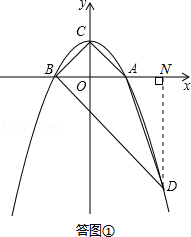
在Rt△BDN中，BN=DN=3，由勾股定理得：BD= 
；
在Rt△ADN中，DN=3，AN=1，由勾股定理得：AD= 
；
又OA=OB=OC=1，OC⊥AB，由勾股定理得：AC=BC= 
；
∴四边形ABCD的周长为：AC+BC+BD+AD= + + + = 
+
方法二
∵A（1，0），C（0，1），∴lAC：y=﹣x+1，
∵BD∥CA，∴KBD=KAC=﹣1，
∴lBD：y=﹣x﹣1，
∴ 
，
∴x1=2，x2=﹣1（舍），
∴D（2，﹣3），
∴AC= 
= ，
CB= 
= ，
BD= 
=3 ，
DA= 
= ，
∴四边形ABCD的周长为：5 +
（3）
解：假设存在这样的点P，则△BPE与△CBD相似有两种情形：
（Ⅰ）若△EPB∽△BDC，如答图②所示，
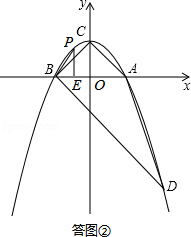
则有 
，即 
，∴PE=3BE．
设OE=m（m＞0），则E（﹣m，0），BE=1﹣m，PE=3BE=3﹣3m，
∴点P的坐标为（﹣m，3﹣3m）．
∵点P在抛物线y=﹣x2+1上，
∴3﹣3m=﹣（﹣m）2+1，解得m=1或m=2，
当m=1时，点E与点B重合，故舍去；当m=2时，点E在OB左侧，点P在x轴下方，不符合题意，故舍去．
因此，此种情况不存在；
（Ⅱ）若△EBP∽△BDC，如答图③所示，
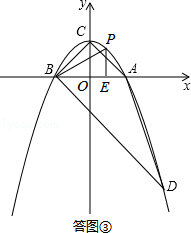
则有 
，即 
，∴BE=3PE．
设OE=m（m＞0），则E（m，0），BE=1+m，PE= 
BE= （1+m）= + m，
∴点P的坐标为（m， + m）．
∵点P在抛物线y=﹣x2+1上，
∴ + m=﹣（m）2+1，解得m=﹣1或m= 
，
∵m＞0，故m=﹣1舍去，∴m= ，
点P的纵坐标为： + m= + × = 
，
∴点P的坐标为（ ， ）．
综上所述，存在点P，使以B、P、E为顶点的三角形与△CBD相似，点P的坐标为（ ， ）
方法二
∵C（0，1），B（﹣1，0），
∴KBC= 
=1，
∵KBD=﹣1，∴KBC×KBD=﹣1，
∴BD⊥BC，
若△EPB∽△BDC，则 
或 
，
①设点P（t，﹣t2+1），E（t，0），B（﹣1，0），
PE=PY=﹣t2+1，BE=EX﹣BX=t+1，
∵BD=3 ，CB= ， ，
∴ 
，
∴t=﹣2（此时点P位于x轴下方，故舍去）
②∵ ，
∴ 
，
∴t= ，
∴P（ ， ）
【解析】（1）利用待定系数法求出抛物线的解析式，点B坐标可由对称性质得到，或令y=0，由解析式得到；（2）关键是求出点D的坐标，然后利用勾股定理分别求出四边形ABCD四个边的长度；（3）本问为存在型问题．可以先假设存在，然后按照题意条件求点P的坐标，如果能求出则点P存在，否则不存在．注意三角形相似有两种情形，需要分类讨论．
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
