题目内容
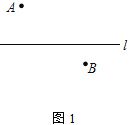
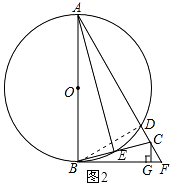
【题目】如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE. 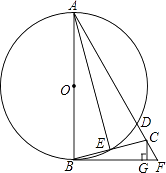
(1)直接写出AE与BC的位置关系;
(2)求证:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半径长.
【答案】
(1)解:如图1,
∵AB是⊙O的直径,
∴∠AEB=90°.
∴AE⊥BC
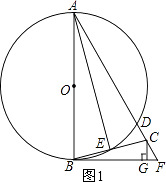
(2)解:如图1,

∵BF与⊙O相切,
∴∠ABF=90°.
∴∠CBF=90°﹣∠ABE=∠BAE.
∵∠BAF=2∠CBF.
∴∠BAF=2∠BAE.
∴∠BAE=∠CAE.
∴∠CBF=∠CAE.
∵CG⊥BF,AE⊥BC,
∴∠CGB=∠AEC=90°.
∵∠CBF=∠CAE,∠CGB=∠AEC,
∴△BCG∽△ACE
(3)解:连接BD,如图2所示.
∵∠DAE=∠DBE,∠DAE=∠CBF,
∴∠DBE=∠CBF.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴BD⊥AF.
∵∠DBC=∠CBF,BD⊥AF,CG⊥BF,
∴CD=CG.
∵∠F=60°,GF=1,∠CGF=90°,
∴tan∠F= ![]() =CG=tan60°=
=CG=tan60°= ![]()
∵CG= ![]() ,
,
∴CD= ![]() .
.
∵∠AFB=60°,∠ABF=90°,
∴∠BAF=30°.
∵∠ADB=90°,∠BAF=30°,
∴AB=2BD.
∵∠BAE=∠CAE,∠AEB=∠AEC,
∴∠ABE=∠ACE.
∴AB=AC.
设⊙O的半径为r,则AC=AB=2r,BD=r.
∵∠ADB=90°,
∴AD= ![]() r.
r.
∴DC=AC﹣AD=2r﹣ ![]() r=(2﹣
r=(2﹣ ![]() )r=
)r= ![]() .
.
∴r=2 ![]() +3.
+3.
∴⊙O的半径长为2 ![]() +3.
+3.
【解析】(1)由AB为⊙O的直径即可得到AE与BC垂直.(2)易证∠CBF=∠BAE,再结合条件∠BAF=2∠CBF就可证到∠CBF=∠CAE,易证∠CGB=∠AEC,从而证到△BCG∽△ACE.(3)由∠F=60°,GF=1可求出CG= ![]() ;连接BD,容易证到∠DBC=∠CBF,根据角平分线的性质可得DC=CG=
;连接BD,容易证到∠DBC=∠CBF,根据角平分线的性质可得DC=CG= ![]() ;设圆O的半径为r,易证AC=AB,∠BAD=30°,从而得到AC=2r,AD=
;设圆O的半径为r,易证AC=AB,∠BAD=30°,从而得到AC=2r,AD= ![]() r,由DC=AC﹣AD=
r,由DC=AC﹣AD= ![]() 可求出⊙O的半径长.
可求出⊙O的半径长.
【考点精析】利用角平分线的性质定理和等腰三角形的判定对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.

 每日10分钟口算心算速算天天练系列答案
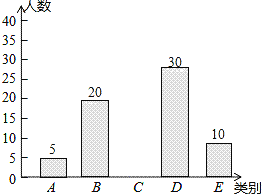
每日10分钟口算心算速算天天练系列答案【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?