题目内容
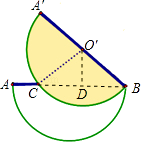
【题目】将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形, ![]() 与直径AB交于点C,连接点C与圆心O′.
与直径AB交于点C,连接点C与圆心O′. 
(1)求 ![]() 的长;
的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白 .
【答案】
(1)解:连结BC,作O′D⊥BC于D,
由题意得,∠CBA′=30°,
则∠BO′C=120°,O′D= ![]() O′B=5,
O′B=5,
∴ ![]() 的长为:
的长为: ![]() =
= ![]()
(2)解:S白= ![]() ×π×102﹣(
×π×102﹣( ![]() ﹣
﹣ ![]() ×10
×10 ![]() ×5)
×5)
=50π﹣ ![]() +25
+25 ![]()
= ![]() π+25
π+25 ![]() .
.
【解析】(1)连结BC,作O′D⊥BC于D,根据旋转变换的性质求出∠CBA′的度数,根据弧长公式计算即可;(2)根据扇形面积公式、三角形面积公式,结合图形计算即可.
【考点精析】本题主要考查了弧长计算公式和扇形面积计算公式的相关知识点,需要掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

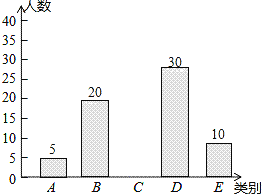
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?
【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) | 豪华(元/间) | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?