题目内容
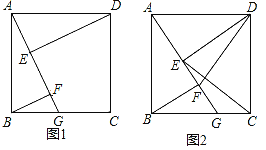
【题目】如图1,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:DE=AF;
(2)若AB=4,BG=3,求AF的长;
(3)如图2,连接DF、CE,判断线段DF与CE的位置关系并证明.
【答案】(1)证明见解析(2)![]() (3)DF⊥CE
(3)DF⊥CE
【解析】
(1)先判断出∠AED=∠BFA=90°,再判断出∠BAF=∠ADE,进而利用“角角边”证明△AFB和△DEA全等,即可得出结论;
(2)先求出AG,再判断出△ABF∽△AGB,得出比例式即可得出结论;
(3)先判断出AD=CD,然后利用“边角边”证明△FAD和△EDC全等,得出∠ADF=∠DCE,即可得出结论.
(1)∵DE⊥AG,BF∥DE,
∴BF⊥AG,
∴∠AED=∠BFA=90°,
∵四边形ABCD是正方形,
∴AB=AD且∠BAD=∠ADC=90°,
∴∠BAF+∠EAD=90°,
∵∠EAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△AFB和△DEA中,
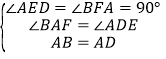 ,
,
∴△AFB≌△DEA(AAS),
∴AF=DE;
(2)在Rt△ABG中,AB=4,BG=3,根据勾股定理得,AG=5,
∵BF⊥AG,
∴∠AFB=∠ABG=90°,
∵∠BAF=∠GAB,
∴△ABF∽△AGB,
∴![]() ,
,
即![]() ,
,
∴AF=![]() ;
;
(3)DF⊥CE,理由如下:
∵∠FAD+∠ADE=90°,∠EDC+∠ADE=∠ADC=90°,
∴∠FAD=∠EDC,
∵△AFB≌△DEA,
∴AF=DE,
又∵四边形ABCD是正方形,
∴AD=CD,
在△FAD和△EDC中,
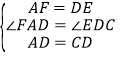 ,
,
∴△FAD≌△EDC(SAS),
∴∠ADF=∠DCE,
∵∠ADF+∠CDF=∠ADC=90°,
∴∠DCE+∠CDF=90°,
∴DF⊥CE.

 阅读快车系列答案
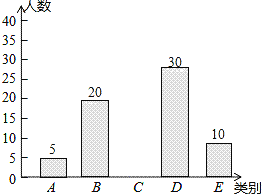
阅读快车系列答案【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?