Question

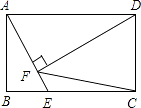
【题目】如图，在平面直角坐标系中，矩形ABCD的顶点A、D在坐标轴上，其坐标分别为（2，0），（0，4），对角线AC⊥x轴．
（1）求直线DC对应的函数解析式
（2）若反比例函数y= （k＞0）的图象经过DC的中点M，请判断这个反比例函数的图象是否经过点B，并说明理由．

Answer 1

【答案】
（1）解：如图所示：过点D作DE⊥AC，垂足为E．

∵DE⊥AC，AC∥y轴，

∴∠EDO=90°．

∴∠EDA+∠ODA=90°．

又∵ABCD为矩形，

∴∠CDE+∠ADE=90°．

∴∠CDE=∠ODA．

又∵∠DOA=∠DEC=90°，

∴△DAO∽△DCE．

∴ = ，即 = ，解得EC=1．

∴C（2，5）．

设直线DC的解析式为y=kx+4，将点C的坐标代入得：2k+4=5，解得k= ．

∴直线CD的解析式为y= x+4

（2）解：过点D作DE⊥AC，过点B作BF⊥AC．

∵DE⊥AC，BF⊥AC．

∴∠DEC=∠BFA=90°．

∵DC∥AB，

∴∠DCE=∠FAB．

在△DEC和△BAF中 ，

∴△DEC≌△BAF．

∴DE=BF=2，EC=AF=1．

∴B（4，1）．

∵D（0，4），C（2，5），

∴CD中点M的坐标为（1， ）．

∴k=1× = ．

∵4×1=4≠ ，

∴点B不在反比例函数图象上

【解析】过点D作DE⊥AC，垂足为E．先证明△DAO∽△DCE，依据相似三角形的性质可求得EC=1，从而可求得EC的长，故此可得到点C的坐标，设直线DC的解析式为y=kx+4，将点C的坐标代入求解即可；（2）过点D作DE⊥AC，过点B作BF⊥AC．先证明△DEC≌△BAF，从而可求得点B的坐标，然后再求得反比例反函数比例系数k的值，然后根据点B的坐标是否符合函数解析式进行判断即可．
【考点精析】通过灵活运用确定一次函数的表达式和矩形的性质，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；矩形的四个角都是直角，矩形的对角线相等即可以解答此题．