题目内容
【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.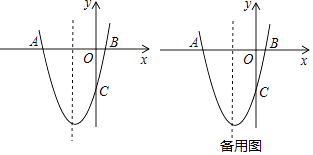
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标.
【答案】
(1)解:由题意,可得A(﹣5,0),C(0,﹣5).
∵抛物线y=x2+bx+c过点A,点C,
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线对应的函数解析式为y=x2+4x﹣5;
(2)解:∵y=x2+4x﹣5=(x+2)2﹣9,
∴对称轴是直线x=﹣2.
∵抛物线y=x2+4x﹣5与x轴交于点A,B,
∴点A,B关于直线x=﹣2对称.
连结AC,交对称轴于点P,此时PB+PC的值最小.

设直线AC的解析式为y=mx+n,
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣x﹣5,
当x=﹣2时,y=﹣3,
∴点P的坐标为(﹣2,﹣3)
(3)解:在(2)条件下,点P的坐标为(﹣2,﹣3).
设F(x,x2+4x﹣5),
∵四边形PEFM为正方形,
∴E(﹣2,x2+4x﹣5),M(x,﹣3),PM=PE,
∴|x+2|=|x2+4x﹣5+3|,
∴x2+4x﹣2=x+2,或x2+4x﹣2=﹣x﹣2,
整理得x2+3x﹣4=0,或x2+5x=0,
解得x1=﹣4,x2=1,x3=0,x4=﹣5,
∴M(﹣4,﹣3)或M(1,﹣3)或M(0,﹣3)或M(﹣5,﹣3)
【解析】(1)由题意,可得A(﹣5,0),C(0,﹣5).把点A,C的坐标代入y=x2+bx+c,得到关于b、c的二元一次方程组,解方程组即可求出抛物线的函数解析式;(2)利用配方法求出抛物线的对称轴是直线x=﹣2.由抛物线y=x2+4x﹣5与x轴交于点A,B,得出点A,B关于直线x=﹣2对称.连结AC,交对称轴于点P,根据两点之间线段最短可知此时PB+PC的值最小.利用待定系数法求出直线AC的解析式为y=﹣x﹣5,把x=﹣2代入,求出y=﹣3,进而得出点P的坐标;(3)在(2)条件下,点P的坐标为(﹣2,﹣3).设F(x,x2+4x﹣5),根据正方形的性质可得E(﹣2,x2+4x﹣5),M(x,﹣3),PM=PE,根据两点间的距离公式列出方程|x+2|=|x2+4x﹣5+3|,解方程即可求解.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 .