Question

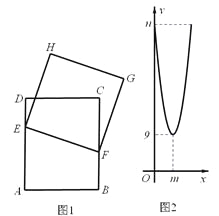
【题目】如图1，A、B、C、D为矩形的四个顶点，AD=4cm，AB=dcm。动点E、F分别从点D、B出发，点E以1 cm/s的速度沿边DA向点A移动，点F以1 cm/s的速度沿边BC向点C移动，点F移动到点C时，两点同时停止移动。以EF为边作正方形EFGH，点F出发xs时，正方形EFGH的面积为ycm2。已知y与x的函数图象是抛物线的一部分，如图2所示。请根据图中信息，解答下列问题：

（1）自变量x的取值范围是 ▲ ；

（2）d= ▲ ，m= ▲ ，n= ▲ ；

（3）F出发多少秒时，正方形EFGH的面积为16cm2？

Answer 1

【答案】（1）0≤x≤4。

（2）3，2，25．

（3）F出发或秒时，正方形EFGH的面积为16cm2

【解析】

（1）自变量x的取值范围是点F从点C到点B的运动时间，由时间=距离÷速度，即可求。

（2）由图2知，正方形EFGH的面积的最小值是9，而正方形EFGH的面积最小时，根据地两平行线间垂直线段最短的性质，得d=AB=EF=3。

当正方形EFGH的面积最小时，由BF=DE和EF∥AB得，E、F分别为AD、BC的中点，即m=2。

当正方形EFGH的面积最大时，EF等于矩形ABCD的对角线，根据勾股定理，它为5，即n=25。

解：（1）0≤x≤4。

（2）3，2，25．

（3）过点E作EI⊥BC垂足为点I。则四边形DEIC为矩形。

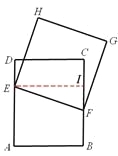
∴EI=DC=3，CI=DE=x。

∵BF=x，∴IF=4－2x。

在Rt△EFI中，。

∵y是以EF为边长的正方形EFGH的面积，

∴。

当y=16时，，

解得，。

∴F出发或秒时，正方形EFGH的面积为16cm2。

（3）求出正方形EFGH的面积y关于x的函数关系式，即可求得F出发或秒时，正方形EFGH的面积为16cm2。