题目内容
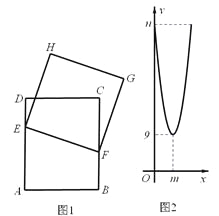
【题目】如图![]() ,已知点G在正方形ABCD的对角线AC上,
,已知点G在正方形ABCD的对角线AC上,![]() ,垂足为点E,
,垂足为点E,![]() ,垂足为点F.
,垂足为点F.
![]() 发现问题:在图
发现问题:在图![]() 中,
中,![]() 的值为______.
的值为______.
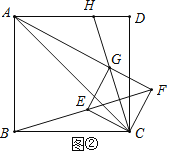
![]() 探究问题:将正方形CEGF绕点C顺时针方向旋转
探究问题:将正方形CEGF绕点C顺时针方向旋转![]() 角
角![]() ,如图
,如图![]() 所示,探究线段AG与BE之间的数量关系,并证明你的结论.
所示,探究线段AG与BE之间的数量关系,并证明你的结论.
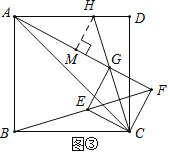
![]() 解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图
解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图![]() 所示,延长CG交AD于点H;若
所示,延长CG交AD于点H;若![]() ,
,![]() ,直接写出BC的长度.
,直接写出BC的长度.
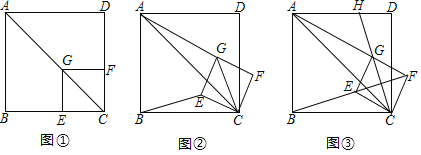
【答案】(1)![]() ;(2)
;(2)![]() ,证明见详解;(3)
,证明见详解;(3)![]() .
.
【解析】
![]() 由正方形的性质可得
由正方形的性质可得![]() ,
,![]() ,可证
,可证![]() ,
,![]() ,可得
,可得![]() ,由平行线分线段成比例可得
,由平行线分线段成比例可得![]() ;
;
![]() 由正方形的性质可得
由正方形的性质可得![]() ,即可证
,即可证![]() ∽
∽![]() ,可得
,可得![]() ,则
,则![]() ;
;
![]() 过点H作
过点H作![]() 于点M,构造等腰
于点M,构造等腰![]() ,利用HG的长度分别求出HM,GM,AH的长度,再利用
,利用HG的长度分别求出HM,GM,AH的长度,再利用![]() 与
与![]() 相似即可求出AC的长度,进一步求出BC的长度.
相似即可求出AC的长度,进一步求出BC的长度.
解:![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() ;
;
![]() ,
,
理由如下:
如图![]() ,
,![]() 四边形ABCD,四边形GECF是正方形,
四边形ABCD,四边形GECF是正方形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
即![]() ,
,
![]() 如图
如图![]() ,过点H作
,过点H作![]() 于点M
于点M
![]() 四边形ABCD,四边形GECF是正方形,
四边形ABCD,四边形GECF是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,
![]() ,
,
![]() ,且
,且![]()
![]() ∽
∽![]()
![]() ,
,
即![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,
![]() ,
,
![]() 的长度为
的长度为![]() .
.
故答案为:(1)![]() ;(2)
;(2)![]() ,证明见详解;(3)
,证明见详解;(3)![]() .
.

【题目】四川省芦山县4月20日发生了7.0级强烈地震,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材48000m2和B种板材24000m2的任务.
⑴如果该厂安排280人生产这两种板材,每人每天能生产A种板材60 m2或B种板材40 m2,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
⑵某灾民安置点计划用该厂生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
甲型 | 110 | 61 | 12 |
乙型 | 160 | 53 | 10 |
①共有多少种建房方案可供选择?
②若这个灾民安置点有4700名灾民需要安置,这400间板房能否满足需要?若不能满足请说明理由;若能满足,请说明应选择什么方案.