题目内容
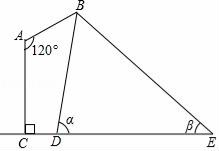
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
【答案】灯杆AB的长度为2米.
【解析】过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.设BF=3x知EF=4x、DF=![]() ,由DE=18求得x=4,据此知BG=BF-GF=1,再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG=2.
,由DE=18求得x=4,据此知BG=BF-GF=1,再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG=2.
过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.

由题意得∠BDE=α,tan∠β=![]() .
.
设BF=3x,则EF=4x
在Rt△BDF中,∵tan∠BDF=![]() ,
,
∴DF=![]() ,
,
∵DE=18,
∴![]() x+4x=18.
x+4x=18.
∴x=4.
∴BF=12,
∴BG=BF-GF=12-11=1,
∵∠BAC=120°,
∴∠BAG=∠BAC-∠CAG=120°-90°=30°.
∴AB=2BG=2,
答:灯杆AB的长度为2米.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】“湖田十月清霜堕,晚稻初香蟹如虎”,又到了食蟹的好季节啦!某经销商去水产批发市场采购牟山湖大闸蟹,他看中了![]() 两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
![]() 家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0-50部分 | 50以上-150的部分 | 150以上-250的部分 | 250以上的部分 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发70千克牟山湖大闸蟹,则他在![]() 两家批发分别需要多少元;
两家批发分别需要多少元;
(2)如果他批发![]() 千克牟山湖大闸蟹(
千克牟山湖大闸蟹(![]() ),请你分别用含字母
),请你分别用含字母![]() 的式子表示他在
的式子表示他在![]() 两家批发所需的费用;
两家批发所需的费用;
(3)现在他要批发180千克山湖大闸蟹,你能帮助他选择哪家批发更便宜吗.请说明理由.
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
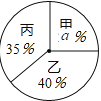
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?