��Ŀ����
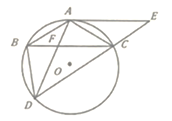
����Ŀ����ͼ1��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=13��BD=24��������ABCD���ⲿ��ABΪ�����ȱ������� ABE����F�ǶԽ���BD��һ���㣨��F�����B�غϣ������߶�AF�Ƶ�A˳ʱ�뷽����ת60���õ��߶�AM������FM��
��1����AO�ij���
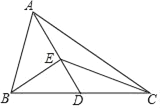
��2����ͼ2������F���߶�BO�ϣ��ҵ�M��F��C������ͬһ��ֱ����ʱ����֤��AC=![]() AM��
AM��
��3������EM������AEM�����Ϊ40����ֱ��д����AFM���ܳ���
���𰸡���1����5����2����֤�����̼���������3����3![]()
��������
�����������1������RT��OAB�У����ù��ɶ���OA=![]() ��⣻��2�������ı���ABCD�����Σ������AFMΪ�ȱ������Σ���M=��AFM=60�����������MAC=90������Rt��ACM��tan��M=
��⣻��2�������ı���ABCD�����Σ������AFMΪ�ȱ������Σ���M=��AFM=60�����������MAC=90������Rt��ACM��tan��M=![]() �����AC����3���������AEM�ա�ABF��������AEM�����Ϊ40���BF�������ù��ɶ���AF=
�����AC����3���������AEM�ա�ABF��������AEM�����Ϊ40���BF�������ù��ɶ���AF=![]() =
=![]() ���ó���AFM���ܳ�Ϊ3
���ó���AFM���ܳ�Ϊ3![]() ��
��
�����������1�������ı���ABCD�����Σ�
��AC��BD��OB=OD=![]() BD��
BD��
��BD=24��
��OB=12��
��Rt��OAB��
��AB=13��
��OA=![]() =5��
=5��
��2������ͼ2��
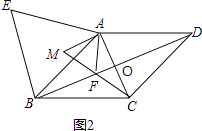
���ı���ABCD�����Σ�
��BD��ֱƽ��AC��
��FA=FC����FAC=��FCA��
����֪AF=AM����MAF=60����
���AFMΪ�ȱ������Σ�
���M=��AFM=60����
����M��F��C������ͬһ��ֱ���ϣ�
���FAC+��FCA=��AFM=60����
���FAC=��FCA=30����
���MAC=��MAF+��FAC=60��+30��=90����
��Rt��ACM����tan��M=![]() ��
��
��tan60��=![]() ��
��
��AC=![]() AM��
AM��
��3������ͼ������EM��
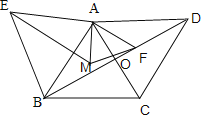
�ߡ�ABE�ǵȱ������Σ�
��AE=AB����EAB=60����
�ɣ�2��֪��AFMΪ�ȱ������Σ�
��AM=AF����MAF=60����
���EAM=��BAF��
����AEM����ABF�� ��
��
���AEM�ա�ABF��SAS����
�ߡ�AEM�����Ϊ40����ABF�ĸ�ΪAO
��![]() BFAO=40��BF=16��
BFAO=40��BF=16��
��FO=BF��BO=16��12=4
AF=![]() =
=![]() ��
��
���AFM���ܳ�Ϊ3![]() ��
��

����Ŀ���Ĵ�ʡ«ɽ��4��20�շ�����7.0��ǿ�ҵ�������Ϊ�˾����巿��������ij���´�������A�ְ��48000m2��B�ְ��24000m2������.
������ó�����280�����������ְ�ģ�ÿ��ÿ��������A�ְ��60 m2��B�ְ��40 m2�����ʣ�Ӧ�ֱ��Ŷ���������A�ְ�ĺ�B�ְ�ģ�����ȷ��ͬʱ��ɸ��Ե���������
��ij�����õ�ƻ��øó����������ְ�Ĵ�ס������ֹ��İ巿��400�䣬��֪����һ����Ͱ巿��һ�����Ͱ巿�����ļ������������±���ʾ��
�巿 | A�ְ��(m2) | B�ְ��(m2) | �������� |
���� | 110 | 61 | 12 |
���� | 160 | 53 | 10 |
�ٹ��ж����ֽ��������ɹ�ѡ��
������������õ���4700��������Ҫ���ã���400��巿�ܷ�������Ҫ��������������˵�����ɣ��������㣬��˵��Ӧѡ��ʲô������