题目内容
【题目】(1)下面是李老师带领同学们探索![]() 的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是
的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是![]() ,且
,且![]() >1,则设
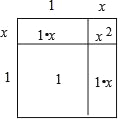
>1,则设![]() =1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即
=1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即![]() =1+x≈ .
=1+x≈ .
(2)请仿照(1)中的方法,若设![]() =1.7+y(0<y<1),求
=1.7+y(0<y<1),求![]() 的近似值(要求画出示意图,标明数据,并将
的近似值(要求画出示意图,标明数据,并将![]() 的近似值精确到千分位)
的近似值精确到千分位)
【答案】(1)2x, 2x+1=2, 0.5,1.5;(2)1.732.
【解析】
(1)解方程即可得到结论;
(2)解方程即可得到结论.
(1)由面积公式,可得x2+2x+1=2.
略去x2,得方程2x+1=2.
解得x=0.5.即![]() ≈1.5;
≈1.5;
故答案为:2x,2x+1=2,0.5,1.5;
(2)由面积公式,可得x2+2×1.7x+1.72=3.
略去x2,得方程2×1.7x+1.72=2.
解得x=0.32.即![]() ≈1.732;
≈1.732;

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目