题目内容
【题目】如图,在△ABC中,AD是△ABC的中线,tanB= ![]() ,cosC=
,cosC= ![]() ,AC=2
,AC=2 ![]() ,求sin∠ADC的值.
,求sin∠ADC的值.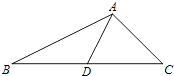
【答案】解:过点A作AH⊥BC交BC与点H,

∵cosC= ![]() ,AC=2
,AC=2 ![]() ,
,
∴AH=2,
∵tanB= ![]() ,
,
∴BH=4,
∵AD是△ABC的中线,
∴DH=1,
∴AD= ![]() =
= ![]() =
= ![]() ,
,
∴sin∠ADC= ![]() =
= ![]() =
= ![]()
![]() .
.
【解析】过点A作AH⊥BC交BC与点H,根据cosC=![]() 及余弦的定义得出AH的值,然后再根据正切的定义及tanB=
及余弦的定义得出AH的值,然后再根据正切的定义及tanB= ![]() ,求出BH的值,根据中线的定义得出DH的值,根据勾股定理得出AD的值,从而可以求出sin∠ADC的值。
,求出BH的值,根据中线的定义得出DH的值,根据勾股定理得出AD的值,从而可以求出sin∠ADC的值。
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对锐角三角函数的定义的理解,了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目