题目内容

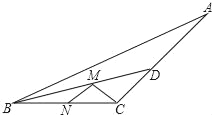
【题目】如图，钝角三角形△ABC的面积是15，最长边AB＝10，BD平分∠ABC，点M，N分别是BD，BC上的动点，则CM+MN的最小值为_____

【答案】3

【解析】

过点C作CE⊥AB于点E，交BD于点M，过点M作MN⊥BC于N，则CE即为CM+MN的最小值，再根据三角形的面积公式求出CE的长，即为CM+MN的最小值．

过点C作CE⊥AB于点E，交BD于点M，过点M作MN⊥BC于N，

∵BD平分∠ABC，ME⊥AB于点E，MN⊥BC于N，

∴MN=ME，

∴CE=CM+ME=CM+MN，

根据垂线段最短可知，CE的长即为CM+MN的最小值，

∵三角形ABC的面积为15，AB=10，

∴×10CE=15，

∴CE=3．

即CM+MN的最小值为3．

故答案为3．

练习册系列答案
相关题目

【题目】定义：P、Q分别是两条线段a和b上任意一点，线段PQ的长度的最小值叫做线段a与线段b的距离． 已知O（0，0），A（4，0），B（m，n），C（m+4，n）是平面直角坐标系中四点．

（1）根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离是；当m=5，n=2时，如图2，线段BC与线段OA的距离为；
（2）如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式．
（3）当m的值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M， ①求出点M随线段BC运动所围成的封闭图形的周长；
②点D的坐标为（0，2），m≥0，n≥0，作MH⊥x轴，垂足为H，是否存在m的值使以A、M、H为顶点的三角形与△AOD相似？若存在，求出m的值；若不存在，请说明理由．

【题目】 如图，数轴上点A对应的有理数为10，点P以每秒1个单位长度的速度从点A出发，点Q以每秒3个单位长度的速度从原点O出发，且P、Q两点同时向数轴正方向运动，设运动时间为t秒．

（1）当t＝2时，P，Q两点对应的有理数分別是　 　，　 　，PQ＝　 　；

（2）当PQ＝8时，求t的值．

【题目】已知：如图，在△ABC中，∠A＝30°，∠B＝60°。

（1）作∠B的平分线BD，交AC于点D；作AB的中点E（要求：尺规作图，保留作图痕迹）

（2）连接DE，求证：△ADE≌△BDE。

【题目】如图，将直角三角形ABC绕其直角顶点C顺时针旋转至△A′B′C′，已知AC＝8，BC＝6，点M，M′分别是AB，A′B′的中点，则MM′的长是(　　)

A. 5 B. 4 C. 3 D. 5

【题目】如图所示，在矩形ABCD中，E是BC上一点，AF⊥DE于点F．

（1）求证：DFCD=AFCE．
（2）若AF=4DF，CD=12，求CE的长．

【题目】(1)下面是李老师带领同学们探索的近似值的过程，请你仔细阅读并补充完整：我们知道，面积是2的正方形的边长是，且＞1，则设＝1+x(0＜x＜1)，可画出如图所示的示意图．由各部分面积之和等于总面积．可列方程为：x2+　 　+1＝2，∵0＜x＜1，∴认为x2是个较为接近于0的数，令x2≈0，因此省略x2后，得到方程：　 　，解得，x＝　 　，即＝1+x≈　 　．

(2)请仿照(1)中的方法，若设＝1.7+y(0＜y＜1)，求的近似值(要求画出示意图，标明数据，并将的近似值精确到千分位)

【题目】对于平面直角坐标系xOy中的线段AB及点P，给出如下定义：

若点P满足PA=PB，则称P为线段AB的“轴点”，其中，当0°＜∠APB＜60°时，称P为线段AB的“远轴点”；当60°≤∠APB≤180°时，称P为线段AB的“近轴点”.

(1)如图1，点A，B的坐标分别为(-2，0)，(2，0)，则在，，， 中，线段AB的“近轴点”是 .

(2)如图2，点A的坐标为(3，0)，点B在y轴正半轴上，且∠OAB=30°.

①若P为线段AB的“远轴点”，直接写出点P的横坐标t的取值范围 ；

②点C为y轴上的动点(不与点B重合且BC≠AB)，若Q为线段AB的“轴点”，当线段QB与QC的和最小时，求点Q的坐标.

【题目】小红根据学习“数与式”积累的经验，想通过“由特殊到一般”的方法探究下面二次根式的运算规律．

下面是小红的探究过程，请补充完整：

(1)具体运算，发现规律．

特例1：，

特例2：，

特例3：，

特例4： (填写一个符合上述运算特征的例子)．

(2)观察、归纳，得出猜想．

如果为正整数，用含的式子表示上述的运算规律为： ．

(3)证明你的猜想．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网